题目内容
12.已知函数y=f(x)=x2+1,则在x=2,△x=0.1时,△y的值为( )| A. | 0.40 | B. | 0.41 | C. | 0.43 | D. | 0.44 |
分析 根据△y=f(x+△x)-f(x),代入数据计算即可.
解答 解:∵f(x)=x2+1,在x=2,△x=0.1,
∴△y=f(x+△x)-f(x)=f(2+0.1)-f(2)=(2.1)2+1-(22+1)=0.41.
故选:B.
点评 本题主要考查了函数的变化率,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点为A(-1,0),右焦点为F2($\sqrt{3}$,0),则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
7.已知e=2.71828…,设函数f(x)=$\frac{1}{2}$x2-bx+alnx存在极大值点x0,且对于b的任意可能取值,恒有极大值f(x0)<0,则下列结论中正确的是( )
| A. | 存在x0=$\sqrt{a}$,使得f(x0)<-$\frac{1}{e}$ | B. | 存在x0=$\sqrt{a}$,使得f(x0)>-e | ||
| C. | a的最大值为e3 | D. | 0<a<e3 |
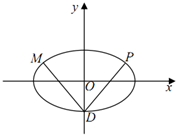 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.