题目内容
12.抛掷一枚均匀的硬币4次,则恰有2次正面向上的概率( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
分析 判断事件是独立重复试验,然后求解即可.
解答 解:抛掷一枚均匀的硬币4次,满足独立重复试验,X~B(4,$\frac{1}{2}$),
则恰有2次正面向上的概率:${C}_{4}^{2}•(\frac{1}{2})^{4}$=$\frac{3}{8}$.
故选:C.
点评 本题考查独立重复试验的应用,基本知识的考查.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20.若长方体的一个顶点上三条棱长分别是1、1、2,且它的八个顶点都在同一球面上,则这个球的表面积是( )
| A. | 6π | B. | 4π | C. | 3π | D. | 12π |
7.某学生记忆导数公式如下,其中错误的一个是( )
| A. | (${\frac{1}{x}}$)′=-$\frac{1}{x^2}$ | B. | (ax)=axlna | C. | (lnx)′=$\frac{1}{x}$ | D. | (sinx)′=-cosx |
4.函数y=x2-(4a+1)x+3a2+3a的图象与x轴交于A、B两点,若两点间的距离等于2,则a的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$或-$\frac{1}{2}$ | D. | $\frac{3}{2}$或-$\frac{2}{3}$ |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点为A(-1,0),右焦点为F2($\sqrt{3}$,0),则双曲线的渐近线方程为( )
| A. | y=±$\sqrt{2}$x | B. | y=±2x | C. | y=±$\frac{\sqrt{2}}{2}$x | D. | y=±$\frac{1}{2}$x |
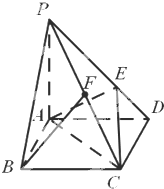 如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°
如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°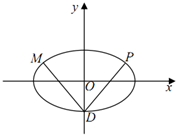 如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.
如图,椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{2\sqrt{2}}{3}$,椭圆C的右焦点到直线x=$\frac{a}{e}$的距离为$\frac{\sqrt{2}}{4}$,椭圆C的下顶点为D.