题目内容

长方体ABCD-A1B1C1D1中，异面直线AB，A1D1所成的角等于
 
．
考点：异面直线及其所成的角
专题：计算题,空间角
分析：欲求异面直线所成角，只需平移异面直线中的一条，是它们成为相交直线，则相交直线所成角即为异面直线所成角，再求出该角即可．
解答： 解：∵在长方体A1B1C1D1-ABCD中，A1D1∥AD，∴AB与AD所成角∠DAB即为异面直线AB与A1D1所成的角．
∵∠DAB=90°，∴异面直线AB与A1D1所成的角等于90°．
故答案为：90°．
点评：本题主要考查异面直线所成角的求法，关键是把异面直线所成角转化为平面角．
练习册系列答案
相关题目
求下列各函数的导数：
（1）y=3x2+xsinx
（2）y=
x2
x+3

（3）y=xcos（2x）
函数y=f（x）是定义在R上的偶函数，且在（-∞，0]上是增函数，设a=f（ln
1
3
），b=f（log43），c=f（0.4-12），则a，b，c的大小关系是
 
．
点M 的柱坐标（4，
π
3
，8）化为直角坐标是
 
．
抛物线y2=ax（a＞0），直线l：x=-
a
4
，过点F（0，
a
4
）作直线l0与抛物线交于A、B两点，过A、B两点作l的垂线垂足为A1、B1，若S △A1AF=4S △B1BF，则直线l0的斜率为
 
．
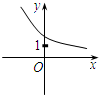f（x）=ax+b的图象如图，其中a、b为常数，则下列结论正确的是
 

①a＞1，b＜0；②a＞1，b＞0；③0＜a＜1，b＞0；④0＜a＜1，b＜0．
已知cos
π
3
=
1
2
，cos
π
5
cos
2π
5
=
1
4
，cos
π
7
cos
2π
7
cos
3π
7
=
1
8
，…
（1）根据以上等式，猜想出一般的结论是
 
；
（2）若数列{an}中，a1=cos
π
3
，a2=cos
π
5
cos
2π
5
，a3=cos
π
7
cos
2π
7
cos
3π
7
，…的前n项和Sn=
1023
1024
，则n=
 
．
在极坐标系中，过点P（2，0）且垂直于极轴的直线方程
 
．
函数f（x）=
4-x
•
x+1
 的定义域是（　　）
A、[-1，+∞）
B、（-∞，-1]
C、[-1，4]
D、（-1，4）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网