题目内容
有7个座位连成一排，安排3人就座，恰有3个空位相邻的不同坐法有（ ）
| A、36种 | B、48种 |
| C、72种 | D、96种 |
考点：计数原理的应用
专题：排列组合
分析：恰有3个空位相邻，用捆绑法，这三个空位一定不和第4个空位相邻，再用插入法，根据分步计数原理可得．
解答：
解：把3个相邻的空位看做一个元素，先安排3人就做，有
=6种，再从3人的间隔中插入两个空位（其中一个是复合元素），故恰有3个空位相邻的不同坐法有
•
=72．
故选：C．
| A | 3 3 |
| A | 3 3 |
| A | 2 4 |
故选：C．
点评：本题考查的是排列问题中的相邻问题，把排列问题包含在实际问题中，解题的关键是看清题目的实质，本题也可以直接表示出所有的满足条件的做法．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
已知等差数列{an}的前n项和是Sn，若S15＞0，S16＜0，则Sn最大值是（ ）
| A、S1 |
| B、S7 |
| C、S8 |
| D、S15 |
微积分基本定理：一般的，如果f（x）是区间[a，b]上的连续函数，并且F′（x）=f（x），那么∫
f（x）dx=（ ）
b a |
| A、F（a）-F（b） |
| B、F（b）-F（a） |
| C、F′（a）-F′（b） |
| D、F′（b）-F′（a） |
有5个不同的小球，装入4个不同的盒内，每盒至少装一个球，共有（ ）不同的装法．
| A、240 | B、120 |
| C、600 | D、360 |
在△ABC中，若a＜b＜c，且c2＜a2+b2，则△ABC为（ ）
| A、直角三角形 | B、锐角三角形 |
| C、钝角三角形 | D、不存在 |
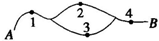如图所示，在A、B间有四个焊接点1，2，3，4，若焊接点脱落导致断路，则电路，则电路不通，今发现A、B之间电路不通，则焊点脱落的不同情况有（ ）| A、9种 | B、11种 |
| C、13种 | D、15种 |
在0°～360°范围内，与-60°终边相同的角是（ ）
| A、30° | B、60° |
| C、300° | D、330° |