题目内容
11.设$f(x)=\left\{{\begin{array}{l}{π,x>0}\\{1,x=0}\\{-π,x<0}\end{array}}\right.,g(x)=\left\{{\begin{array}{l}{1,x为有理数}\\{{{log}_{\frac{1}{2}}}π,x为无理数}\end{array}}\right.$,则f(g(π))的值为( )| A. | 1 | B. | π | C. | -π | D. | 没有正确答案 |
分析 由函数性质得g(π)=$lo{g}_{\frac{1}{2}}π$,从而f(g(π))=f($lo{g}_{\frac{1}{2}}π$),由此能求出结果.
解答 解:∵$f(x)=\left\{{\begin{array}{l}{π,x>0}\\{1,x=0}\\{-π,x<0}\end{array}}\right.,g(x)=\left\{{\begin{array}{l}{1,x为有理数}\\{{{log}_{\frac{1}{2}}}π,x为无理数}\end{array}}\right.$,
∴g(π)=$lo{g}_{\frac{1}{2}}π$,
∴f(g(π))=f($lo{g}_{\frac{1}{2}}π$)=-π.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
1.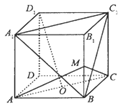 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )| A. | D1O∥平面A1BC1 | B. | D1O⊥平面MAC | ||
| C. | 异面直线BC1与AC所成的角为60° | D. | MO与底面所成角为90° |
19.下列四组函数中表示相等函数的是( )
| A. | f(x)=$\sqrt{{x}^{2}}$,g(x)=x | B. | f(x)=x,g(x)=$\frac{{x}^{2}}{x}$ | ||
| C. | f(x)=lnx2,g(x)=2lnx | D. | f(x)=logaax(a>0,a≠1),g(x)=$\root{3}{{x}^{3}}$ |
16.函数f(x)=2x+5x的零点所在大致区间为( )
| A. | (0,1) | B. | (1,2) | C. | (-1,0) | D. | (-2,-1) |
3.若($\root{n}{-3}$)n有意义,则n一定是( )
| A. | 正偶数 | B. | 正整数 | C. | 正奇数 | D. | 整数 |
20.设Sn是等差数列{an}的前n项和,若$\frac{a_5}{a_3}$=2,则$\frac{S_9}{S_5}$=( )
| A. | $\frac{18}{5}$ | B. | $\frac{14}{5}$ | C. | $\frac{12}{5}$ | D. | $\frac{9}{5}$ |
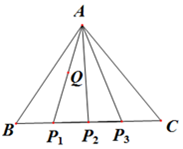 设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).
设△ABC是边长为1的正三角形,点P1,P2,P3四等分线段BC(如图所示).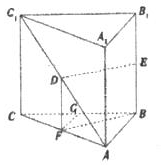 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.