题目内容
6.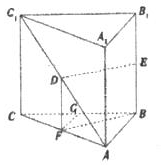 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=$\sqrt{3}$,D、E分别是AC1和BB1的中点,则直线BF与平面BB1C1C所成的角为30°.
分析 取AC的中点为F,连接BF、DF.根据题意得ED∥BF,进而得到直线DE与平面BB1C1C所成的角等于直线BF与平面BB1C1C所成的角,从而可得结论.
解答 解:取AC的中点为F,连接BF、DF.
∵在直三棱柱ABC-A1B1C1中,且D,E分别是AC1和BB1的中点,
∴ED∥BF.
过点F作FG垂直于BC交BC于点G,由题意得∠FBG即为所求的角.
∵AB=1,AC=2,∠ABC=90°,
∴∴∠BCA=30°,
∴在△FBG中∠FBG=30°.
故答案为30°.
点评 本题考查线面角,考查学生的计算能力,解决此类问题的关键是熟悉线面角的作法,即由线上的一点作平面的垂线再连接斜足与垂足则得到线面角.

练习册系列答案
相关题目
16.已知函数f(x)=$\left\{\begin{array}{l}{lgx,x>0}\\{{3}^{x-1},x≤0}\end{array}\right.$,则f(f(1))=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | 1 | D. | $\frac{1}{9}$ |
1.已知函数f(x)=4x2-kx-8在[2,10]上具有单调性,则k的取值范围是( )
| A. | (-∞,-80]∪[-16,+∞) | B. | [-80,-16] | C. | (-∞,16]∪[80,+∞) | D. | [16,80] |
18.若幂函数f(x)的图象经过点(3,9),那么函数f(x)的单调增区间是( )
| A. | [3,+∞) | B. | [0,+∞) | C. | (-∞,0] | D. | (-∞,3] |