经过圆x2+(y+1)2=1的圆心C.且与直线2x+3y-4=0平行的直线方程为( ) A.2x+3y+3=0B.2x+3y-3=0C.2x+3y+2=0D.3x-2y-2=0 题目和参考答案——青夏教育精英家教网—

题目内容

经过圆x²+（y+1）²=1的圆心C，且与直线2x+3y-4=0平行的直线方程为（　　）

A、2x+3y+3=0

B、2x+3y-3=0

C、2x+3y+2=0

D、3x-2y-2=0

考点：圆的标准方程

专题：直线与圆

分析：：设所求直线的方程为 2x+3y+c=0，把圆心C（0，-1）代入求得 c的值，可得所求的直线的方程．

解答： 解：设所求直线的方程为 2x+3y+c=0，把圆心C（0，-1）代入可得 0-3+c=0，求得 c=3，
故所求的直线的方程为 2x+3y+3=0，
故选：A．

点评：本题主要考查利用待定系数法求直线的方程，利用了和直线ax+by+c=0平行的直线一定是ax+by+c′=0的形式，属于基础题．

练习册系列答案

口算题卡加应用题专项沈阳出版社系列答案

将一张坐标纸折叠1次，使点（0，2）与点（-2，0）重合，且点（2008，2009）与点（m，n）重合，则n-m=

．

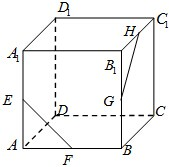如图，在正方体ABCDA₁B₁C₁D₁中，E、F、G、H分别为AA₁、AB、BB₁、BC₁的中点，则异面直线EF与GH所成的角等于（　　）

A、30°	B、45°
C、60°	D、90°

样本（x₁，x₂，…，x_n）的平均数为x，样本（y₁，y₂，…，y_n）的平均数为y（y≠x），样本（x₁，x₂，…，x_n，y₁，y₂，…，y_n）的平均数z=λx+μy，若直线l：（λ+2）x-（1+2μ）y+1-3λ=0，则下列叙述不正确的有
①直线l恒过定点（1，1）；
②直线l与圆　（x-1）²+（y-1）²=4相交；
③直线l到原点的最大距离为

；
④直线l与直线l′：（2λ-3）x-（3-μ）y=0垂直．（　　）

在△ABC中，已知sinB=2sin（B+C）cosC，那么△ABC一定是（　　）

下列函数在（1，+∞）上是增函数的是（　　）

试题分类