题目内容
已知幂函数过点(2,
),则该函数解析式是 .
| 2 |
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:根据题意,设出幂函数的解析式,代入点的坐标,求出幂函数解析式.
解答:
解:设幂函数的解析式为y=xα(α∈R),
∵幂函数过点(2,
),
∴2α=
,
解得α=
;
∴该函数解析式是y=x
(x≥0).
故答案为:y=x
(x≥0).
∵幂函数过点(2,
| 2 |
∴2α=
| 2 |
解得α=
| 1 |
| 2 |
∴该函数解析式是y=x
| 1 |
| 2 |
故答案为:y=x
| 1 |
| 2 |
点评:本题考查了幂函数的定义与应用问题,解题时应用待定系数法,是基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
若直线y=x+b与曲线x=3-
有公共点,则b的取值范围是( )
| 4y-y2 |
A、[-1-2
| ||||
B、[-3,-1+2
| ||||
C、[-1-2
| ||||
D、[-3,-1+
|
函数f(x)是定义在R上的奇函数,并且当x∈(0,+∞)时,f(x)=lnx,那么,f(-e2)=( )
| A、-2 | B、2 | C、1 | D、无法确定 |
已知函数f(x)=xa,且满足f(9)=3,则f(100)=( )
| A、10 | B、100 |
| C、1000 | D、10000 |
某算法程序框图如图所示,若a=
,b=3
,c=log23,则x=( )

| 3 |
| 2 |
| 1 |
| 3 |

A、
| ||
| B、a | ||
| C、b | ||
| D、c |
设a=log0.32,b=0.20.3,c=30.2,则a,b,c的大小关系是( )
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<c<a |
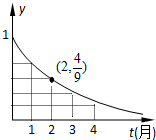 如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述:
如图,是某受污染的湖泊在自然净化过程中,某种有害物质的剩留量y与净化时间t(月)的近似函数关系:y=at(a>0,a≠1,t≥0),有以下叙述: