题目内容

已知两点A（1，0），B（1，
3
），O为坐标原点，点C在第二象限，且∠AOC=120°，设
OC
=-2，
OA
+λ
OB
，（λ∈R），则λ等于（　　）
A、-1B、2C、1D、-2
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：根据已知条件可以求出C点坐标C（λ-2，
3
λ），再根据∠AOC=120°，便有tan120°=
3
λ
λ-2
=-
3
，所以解得λ=1．
解答： 解：
OC
=-2
OA
+λ
OB
=-2(1，0)+λ(1，
3
)=(λ-2，
3
λ)；
即C(λ-2，
3
λ)，又∠AOC=120°所以：
tan120°=
3
λ
λ-2
，解得λ=1．
故选C．
点评：考查向量加法、数乘的坐标运算，以及正切函数的定义．
练习册系列答案
相关题目
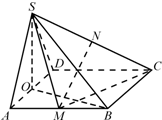四棱锥S-ABCD中，侧面SAD是正三角形，底面ABCD是正方形，且平面SAD⊥平面ABCD，M、N、O分别是AB、SC、AD的中点．
（Ⅰ）求证：MN∥平面SAD；
（Ⅱ）求证：平面SOB⊥平面SCM．
已知F是双曲线
x2
a2
-
y2
4
=1的左焦点，双曲线右支上一动点P，且PD⊥x轴，D为垂足，若线段|FP|-|PD|的最小值为2
5
，则双曲线的离心率为（　　）
A、
3
5
B、2
5
C、
5
2
D、
5
若数列{An}中a1，a2，…an满足|ak+1-ak|=1（k=1，2，…，n-1），则称{An}为E数列，记S（An）=a1+a2+…an．
（1）写出一个E数列{An}满足a1=a9=0且S（A9）＜0；
（2）若a1=2，且E数列{An}是递增数列，数列{bn}中，bn=
1
an•an+1
，数列{bn}的前n项和为Sn．求证：Sn＜
1
2
．
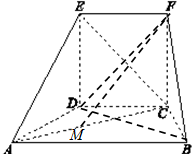如图，所示的几何体中，四边形CDEF为正方形，四边形ABCD为等腰梯形，AB∥CD，AC=
3
，AB=2BC=2，AC⊥FB
（1）求证：AC⊥平面FBC
（2）若M为线段AC的中点，求证：EA∥平面FDM．
已知底面是正三角形，且三条侧陵相等的三棱柱P-ABC，点P，A，B，C都在同一个球面上，若PA，PB，PC两两互相垂直，且球心到截面ABC的距离为
3
3
，则该球的表面积为
 
．
已知等差数列{an}满足：a1+a5=14，a3+a9=26，其前n项和为Sn．
（1）求an和Sn；
（2）若bn=
1
2Sn+1-3an-3
（n∈N+），求数列{bn}的前n项和Tn．
已知集合S={a1，a2，a3，…，an}（n≥3），集合T⊆{（x，y）|x∈S，y∈S，x≠y}且满足：?ai，aj∈S（i，j=1，2，3，…，n，i≠j），（ai，aj）∈T与（aj，ai）∈T恰有一个成立．对于T定义dT（a，b）=
1，(a，b)∈T
0，(b，a)∈T
lT（ai）=dT（ai，a1）+dT（ai，a2）+…+dT（ai，ai-1）+dT（ai，ai+1）+…+dT（ai，an）（i=1，2，3，…，n）．
（Ⅰ）若n=4，（a1，a2），（a3，a2），（a2，a4）∈T，求lT（a2）的值及lT（a4）的最大值；
（Ⅱ）从lT（a1），lT（a2），…，lT（an）中任意删去两个数，记剩下的n-2个数的和为M．求证：M≥
1
2
n（n-5）+3；
（Ⅲ）对于满足lT（ai）＜n-1（i=1，2，3，…，n）的每一个集合T，集合S中是否都存在三个不同的元素e，f，g，使得dT（e，f）+dT（f，g）+dT（g，e）=3恒成立，并说明理由．
设f（x）=（x+1）+（x+1）2+…+（x+1）n，且f（x）中所有项的系数和为An，则
lim
n→∞
An
2n
的值为（　　）
A、2
B、
1
2
C、-
1
2
D、-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网