题目内容
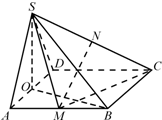 四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N、O分别是AB、SC、AD的中点.
四棱锥S-ABCD中,侧面SAD是正三角形,底面ABCD是正方形,且平面SAD⊥平面ABCD,M、N、O分别是AB、SC、AD的中点.(Ⅰ)求证:MN∥平面SAD;
(Ⅱ)求证:平面SOB⊥平面SCM.
考点:平面与平面垂直的判定,直线与平面平行的判定
专题:证明题,空间位置关系与距离
分析:(Ⅰ)取SD的中点R,连结AR、RN,先证明四边形AMNR是平行四边形,可得MN∥AR,由于AR?平面SAD,MN在平面SAD外,可证MN∥平面SAD.
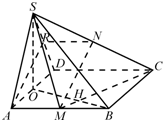
(Ⅱ)如图,设OB∩CM=H,先证明CM⊥SO,再证明CM⊥OB,可证平面SOB⊥平面SCM.
(Ⅱ)如图,设OB∩CM=H,先证明CM⊥SO,再证明CM⊥OB,可证平面SOB⊥平面SCM.
解答:
 (本小题满分12分)
(本小题满分12分)
解:(Ⅰ)如图,取SD的中点R,连结AR、RN,
则RN∥CD,且RN=
CD,AM∥CD,
所以RN∥AM,且RN=AM,
所以四边形AMNR是平行四边形,
所以MN∥AR,由于AR?平面SAD,MN在平面SAD外,
所以MN∥平面SAD.(6分)
(Ⅱ)如图,设OB∩CM=H,由SO⊥AD,面SAD⊥面ABCD,
所以SO⊥平面ABCD,所以CM⊥SO,
易得△ABO≌△BCM,所以∠ABO=∠BCM,
则∠BMH+∠ABO=∠BMH+∠BCM=90°,
所以CM⊥OB,
所以CM⊥平面SOB,因为CM?平面SCM,
所以平面SOB⊥平面SCM.(12分)
 (本小题满分12分)
(本小题满分12分)解:(Ⅰ)如图,取SD的中点R,连结AR、RN,
则RN∥CD,且RN=
| 1 |
| 2 |
所以RN∥AM,且RN=AM,
所以四边形AMNR是平行四边形,
所以MN∥AR,由于AR?平面SAD,MN在平面SAD外,
所以MN∥平面SAD.(6分)
(Ⅱ)如图,设OB∩CM=H,由SO⊥AD,面SAD⊥面ABCD,
所以SO⊥平面ABCD,所以CM⊥SO,
易得△ABO≌△BCM,所以∠ABO=∠BCM,
则∠BMH+∠ABO=∠BMH+∠BCM=90°,
所以CM⊥OB,
所以CM⊥平面SOB,因为CM?平面SCM,
所以平面SOB⊥平面SCM.(12分)
点评:本题主要考察了平面与平面垂直的判定,直线与平面平行的判定,属于中档题.

练习册系列答案
相关题目
若tanα=2,则sin2α值.
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |