题目内容
4.若函数f(x)=$\frac{2\sqrt{2}sin(2x+\frac{π}{4})+(x+2)^{2}-4co{s}^{2}x}{{x}^{2}+2}$的值域为[m,n],则m+n=2.分析 由f(x)化简整理可得1+$\frac{4x+2sin2x}{{x}^{2}+2}$,设g(x)=$\frac{4x+2sin2x}{{x}^{2}+2}$,定义域为R,判断为奇函数,即有最值之和为0,可得m+n=2.
解答 解:函数f(x)=$\frac{2\sqrt{2}sin(2x+\frac{π}{4})+(x+2)^{2}-4co{s}^{2}x}{{x}^{2}+2}$
=$\frac{2\sqrt{2}(\frac{\sqrt{2}}{2}sin2x+\frac{\sqrt{2}}{2}cos2x)-2(1+cos2x)+(x+2)^{2}}{{x}^{2}+2}$
=$\frac{2sin2x-2+{x}^{2}+4x+4}{{x}^{2}+2}$=1+$\frac{4x+2sin2x}{{x}^{2}+2}$,
设g(x)=$\frac{4x+2sin2x}{{x}^{2}+2}$,定义域为R,
g(-x)=$\frac{-4x-2sin2x}{{x}^{2}+2}$=-g(x),
则g(x)为R上的奇函数,
由题意f(x)的值域为[m,n},
即有g(x)=f(x)-1的值域为[m-1,n-1],
由奇函数的性质可得m-1+n-1=0,
即m+n=2.
故答案为:2.
点评 本题考查函数的值域问题,考查函数的奇偶性的运用,注意运用奇函数在R上的最值之和为0,考查运算能力,属于中档题.

练习册系列答案
相关题目
16.一个三棱锥的三视图如图所示,则该三棱锥的体积为( )
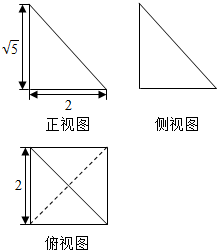

| A. | $\frac{2\sqrt{5}}{3}$ | B. | $\frac{4\sqrt{5}}{3}$ | C. | 4$\sqrt{5}$ | D. | 2$\sqrt{5}$ |
14.直线l过定点(-1,2)且在两坐标轴上的截距相等,则直线l的方程为( )
| A. | 2x+y=0或x+y-1=0 | B. | 2x-y=0或x+y-1=0 | ||
| C. | 2x+y=0或x-y+3=0 | D. | x+y-1=0或x-y+3=0 |