已知双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1的一个焦点是(2.0).则其渐近线的方程为( )A．x±$\sqrt{3}$y=0B．$\sqrt{3}$x±y=0C．x±3y=0D．3x±y=0 题目和参考答案——青夏教育精英家教网—

题目内容

1．已知双曲线x²-$\frac{{y}^{2}}{{b}^{2}}$=1（b＞0）的一个焦点是（2，0），则其渐近线的方程为（　　）

A．

x±$\sqrt{3}$y=0

B．

$\sqrt{3}$x±y=0

C．

x±3y=0

D．

3x±y=0

分析由题意可得c=2，即1+b²=4，解得b，进而得到双曲线的方程，即可得到渐近线方程．

解答解：由题意可得c=2，即1+b²=4，
解得b=$\sqrt{3}$，
可得渐近线方程为y=±$\sqrt{3}$x．
故选B．

点评本题考查双曲线的方程和渐近线方程的求法，注意运用双曲线的基本量的关系和渐近线方程与双曲线的方程的关系，考查运算能力，属于基础题．

练习册系列答案

相关题目

11．已知l为一条直线，α，β为两个不同的平面，则下列说法正确的是（　　）

12．在△ABC中，角A，B，C所对的边分别为a，b，c，且cos2A+cos2B+2sinAsinB=2coc²C．
（Ⅰ）求角C的值；
（Ⅱ）若△ABC为锐角三角形，且$c=\sqrt{3}$，求a-b的取值范围．

9．如图1，等腰梯形BCDP中，BC∥PD，BA⊥PD于点A，PD=3BC，且AB=BC=1．沿AB把△PAB折起到△P'AB的位置（如图2），使∠P'AD=90°．

（Ⅰ）求证：CD⊥平面P'AC；
（Ⅱ）求三棱锥A-P'BC的体积；
（Ⅲ）线段P'A上是否存在点M，使得BM∥平面P'CD．若存在，指出点M的位置并证明；若不存在，请说明理由．

16．

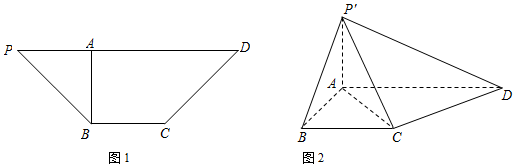
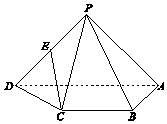如图，在四棱锥P-ABCD中，AD∥BC，∠BAD=90°，PA=PD，AB⊥PA，AD=2，AB=BC=1
（Ⅰ）求证：平面PAD⊥平面ABCD
（Ⅱ）若E为PD的中点，求证：CE∥平面PAB
（Ⅲ）若DC与平面PAB所成的角为30°，求四棱锥P-ABCD的体积．

6．已知圆（x-1）²+y²=4与抛物线y²=2px（p＞0）的准线相切，则p=2．

13．设不等式$\left\{\begin{array}{l}x≥1\\ x-y≤0\\ x+y≤4\end{array}\right.$表示的平面区域为M，若直线y=kx-2上存在M内的点，则实数k的取值范围是[2，5]．

10．已知幂函数y=f（x）过点（2，8），则f（3）=（　　）

20．函数f（x）=log₃（2x-1）的零点是（　　）

试题分类