题目内容
8．在△ABC中，角A，B，C的对边分别为a，b，c．若c=3，C=$\frac{π}{3}$，sinB=2sinA，则a=$\sqrt{3}$．分析 利用由正弦定理可得b=2a，再由余弦定理可得c2=a2+b2-2ab•cosC，由此求得a的值．
解答 解：△ABC中，∵c=3，C=$\frac{π}{3}$，sinB=2sinA，∴由正弦定理可得b=2a．
再由余弦定理可得c2=a2+b2-2ab•cosC，即9=a2+4a2-2a•2a•cos$\frac{π}{3}$，
求得a=$\sqrt{3}$，
故答案为：$\sqrt{3}$．
点评 此题考查学生灵活运用正弦、余弦定理化简求值，灵活运用三角形的面积公式化简求值，是一道基础题．
练习册系列答案
相关题目
19．下列函数中既是奇函数又在区间（0，+∞）上单调递减的是（ ）
| A． | y=e-x | B． | y=ln（-x） | C． | y=x3 | D． | $y=\frac{1}{x}$ |
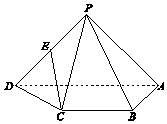如图，在四棱锥P-ABCD中，AD∥BC，∠BAD=90°，PA=PD，AB⊥PA，AD=2，AB=BC=1