题目内容
5.已知函数f(x)=ex,g(x)=x+1,则关于f(x),g(x)的语句为假命题的是( )| A. | ?x∈R,f(x)>g(x) | B. | ?x1,x2∈R,f(x1)<g(x2) | ||
| C. | ?x0∈R,f(x0)=g(x0) | D. | ?x0∈R,使得?x∈R,f(x0)-g(x0)≤f(x)-g(x) |
分析 根据全称命题和特称命题的定义进行判断即可.
解答 解:设h(x)=f(x)-g(x),则h(x)=ex-x-1,
则h′(x)=ex-1,
当x<0时,h′(x)<0,h(x)单调递减,
当x>0时,h′(x)>0,则h(x)单调递增,
即当x=0时,函数h(x)取得极小值同时也是最小值h(0)=0,
即h(x)≥0,即?x∈R,f(x)>g(x)不一定成立,故A是假命题,
故选:A
点评 本题主要考查命题的真假判断,构造函数,求函数的导数,判断函数的单调性和最值是解决本题的关键.

练习册系列答案
相关题目
16.已知函数f(x)=-cos2x-8sinx+9.则函数f(x)的最小值为( )
| A. | 2 | B. | 0 | C. | 18 | D. | -2 |
17.已知集合A={x|y=$\sqrt{4-{x}^{2}}$},B={x|a≤x≤a+1},若A∪B=A,则实数a的取值范围为( )
| A. | (-∞,-3]∪[2,+∞) | B. | [-1,2] | C. | [-2,1] | D. | [2,+∞) |
14. 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=1处的切线方程为4x-2y-5=0,记g(x)=$\frac{1}{f′(x)}$,程序框图如图所示,若输出的结果S>$\frac{2011}{2012}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=1处的切线方程为4x-2y-5=0,记g(x)=$\frac{1}{f′(x)}$,程序框图如图所示,若输出的结果S>$\frac{2011}{2012}$,则判断框中可以填入的关于n的判断条件是( )
 已知函数f(x)=ax3+$\frac{1}{2}$x2在x=1处的切线方程为4x-2y-5=0,记g(x)=$\frac{1}{f′(x)}$,程序框图如图所示,若输出的结果S>$\frac{2011}{2012}$,则判断框中可以填入的关于n的判断条件是( )
已知函数f(x)=ax3+$\frac{1}{2}$x2在x=1处的切线方程为4x-2y-5=0,记g(x)=$\frac{1}{f′(x)}$,程序框图如图所示,若输出的结果S>$\frac{2011}{2012}$,则判断框中可以填入的关于n的判断条件是( )| A. | n≤2011? | B. | n>2011? | C. | n≤2012? | D. | n>2012? |
15.程序框图如图,该程序运行后,为使输出的y≤256,则循环体的判断框内①处应填( )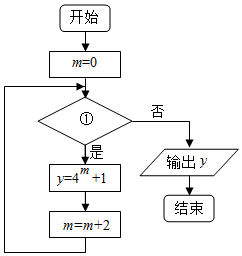

| A. | m<2? | B. | m≤2? | C. | m≤3? | D. | m≤4? |