题目内容
20.在△ABC中,己知a,b,c满足(a+b+c)(a-b+c)=ac,求∠B的大小.分析 由题中等式,化简出a2+c2-b2=-ac,再根据余弦定理算出cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$的值,结合三角形内角的范围即可算出角B的大小.
解答 解:∵在△ABC中,(a+b+c)(a-b+c)=ac,
∴(a+c)2-b2=ac,整理得a2+c2-b2=-ac,
由余弦定理,得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=-$\frac{1}{2}$,
结合B∈(0,π),可得:B=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题给出三角形边之间的关系,求角的大小.着重考查了利用余弦定理解三角形的知识,属于基础题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
15.程序框图如图,该程序运行后,为使输出的y≤256,则循环体的判断框内①处应填( )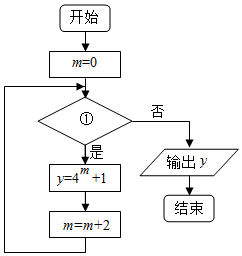

| A. | m<2? | B. | m≤2? | C. | m≤3? | D. | m≤4? |
5.函数y=sinx•tanx的图象大致是( )
| A. |  | B. |  | C. |  | D. | 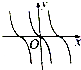 |