题目内容
15.2015年9月3日起,我国在北京举办了包括阅兵式在内的多种话动以纪念抗战胜剩70周年,某五国领导人A,B,C,D,E也应邀参加了观礼活动,活动期间,这五位领导人中,除B与E,D与E不单独会晤外,其他领导人两两之间郡要单独会晤,现安排他们在两天的上午,下午单独会晤(每人每个半天最多只进行一次会晤,每个半天安排两场会晤同时进行),那么安排他们单独会晤的不同方法共有( )| A. | 96种 | B. | 36种 | C. | 24种 | D. | 48种 |
分析 单独会晤,共有AB,AC,AD,AE,BC,BD,CD,CE共8种情况,再分步,即可得出结论.
解答 解:单独会晤,共有AB,AC,AD,AE,BC,BD,CD,CE共8种情况,设为第n次,分成四个时段,每个时段[即某个上午或下午]有两次,各个时段没有关系.
设第一次会晤有E,则有两种方法(不防设为AE),
则第二次会晤在BCD内任选(设为BD),有三种方法,
第三次设再有E则有一种方法(CE),
第四次在ABD内任选则有两种方法(设为AD),
则剩下的排序只有4种,则有2×3×1×2×4=48种.
故选:D.
点评 本题考查计数原理的运用,考察学生分析解决问题的能力,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
9.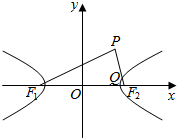 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{\sqrt{5}}{5}x$ | B. | y=±$\frac{1}{2}x$ | C. | y=±$\frac{\sqrt{3}}{2}x$ | D. | y=±$\frac{\sqrt{3}}{3}x$ |
10.已知命题P:?x∈R,mx2+1<1;q:?x∈R,x2+mx+1≥0,若p∨(¬q)为假命题,则实数m的取值范围是( )
| A. | (-∞,0)∪(2,+∞) | B. | [0,2] | C. | [2,+∞) | D. | [-2,0] |
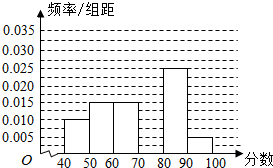 某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题: