题目内容
1.对a,b∈R,记min{a,b}=$\left\{\begin{array}{l}{a,a≤b}\\{b,a>b}\end{array}\right.$,函数f(x)=min{-|x|,-x2+4x+6}的最大值是( )| A. | 6 | B. | 1 | C. | 0 | D. | $\frac{3-\sqrt{33}}{2}$ |
分析 讨论当-|x|≤-x2+4x+6,当-|x|>-x2+4x+6,可得f(x)的解析式,再由绝对值函数和二次函数的单调性即可得到所求最大值.
解答 解:当-|x|≤-x2+4x+6,即为
$\left\{\begin{array}{l}{x≥0}\\{{x}^{2}-5x-6≤0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{{x}^{2}-3x-6≤0}\end{array}\right.$,
即有0≤x≤6或$\frac{3-\sqrt{33}}{2}$≤x<0,
即$\frac{3-\sqrt{33}}{2}$≤x≤6时,
f(x)=min{-|x|,-x2+4x+6}=-|x|,
当x=0时,取得最大值0;
当-|x|>-x2+4x+6,即为x>6或x<$\frac{3-\sqrt{33}}{2}$时,
可得f(x)=-x2+4x+6=-(x-2)2+10,
由f(6)=-6,f($\frac{3-\sqrt{33}}{2}$)=$\frac{3-\sqrt{33}}{2}$,
-6<$\frac{3-\sqrt{33}}{2}$,可得f(x)的值域为(-∞,$\frac{3-\sqrt{33}}{2}$).
即有f(x)的最大值为0.
故选C.
点评 本题考查分段函数的运用,考查函数的最值的求法,注意运用分类讨论的思想方法,考查运算能力,属于中档题.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
9.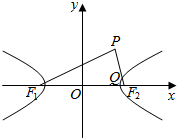 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
 如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )
如图,已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点,点P在第一象限,且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$,($\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$)•$\overrightarrow{{F}_{2}P}$=0,线段PF2与双曲线C交于点Q,若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$,则双曲线C的渐近线方程为( )| A. | y=±$\frac{\sqrt{5}}{5}x$ | B. | y=±$\frac{1}{2}x$ | C. | y=±$\frac{\sqrt{3}}{2}x$ | D. | y=±$\frac{\sqrt{3}}{3}x$ |
16.圆锥的轴截面SAB是边长为4的正三角形(S为顶点),O为底面中心,M为SO中点,动点P在圆锥底面内(包括圆周),若AM⊥MP,则点P形成的轨迹长度为( )
| A. | $\frac{\sqrt{7}}{3}$ | B. | $\frac{\sqrt{7}}{2}$ | C. | $\frac{2}{5}\sqrt{7}$ | D. | $\sqrt{7}$ |
13.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x},x>0}\\{x+1,x≤0}\end{array}\right.$,则f(-2)=( )
| A. | -1 | B. | 0 | C. | $\frac{1}{4}$ | D. | 4 |
10.已知命题P:?x∈R,mx2+1<1;q:?x∈R,x2+mx+1≥0,若p∨(¬q)为假命题,则实数m的取值范围是( )
| A. | (-∞,0)∪(2,+∞) | B. | [0,2] | C. | [2,+∞) | D. | [-2,0] |
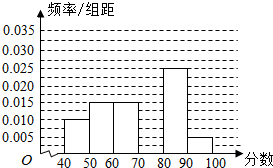 某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题:
某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50)、[50,60)、…、[90,100)后得到如图所示的频率分布直方图.观察图形的信息,回答下列问题: