题目内容
15.已知某海港的货运码头只能停泊一艘货轮,甲、乙两艘货轮都要在此码头停靠6小时,假定它们在一昼夜的时间段中随机到达,求这两艘货轮中有一艘货轮停泊在此码头,另一艘货轮等待的概率.分析 设出甲、乙到达的时刻,列出所有基本事件的约束条件同时列出这两艘船中至少有一艘在停靠泊位时必须等待约束条件,利用线性规划作出平面区域,利用几何概型概率公式求出概率.
解答 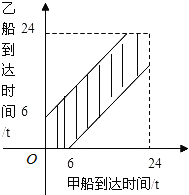 解:设甲到达的时刻为x,乙到达的时刻为y则所有的基本事件构成的区域
解:设甲到达的时刻为x,乙到达的时刻为y则所有的基本事件构成的区域
Ω=$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\end{array}\right.$,其面积SΩ=242,如图所示
这两艘船中至少有一艘在停靠泊位时必须等待包含的基本事件构成的区域
A=$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\\{|x-y|≤6}\end{array}\right.$,即图中阴影部分,其面积为SA=242-182,
这两艘船中至少有一艘在停靠泊位时必须等待的概率P(A)=$\frac{2{4}^{2}-1{8}^{2}}{2{4}^{2}}$=$\frac{7}{16}$.
点评 本题主要考查建模、解模能力;解答关键是利用线性规划作出事件对应的平面区域,再利用几何概型概率公式求出事件的概率.

练习册系列答案
相关题目
10.已知命题P:?x∈R,mx2+1<1;q:?x∈R,x2+mx+1≥0,若p∨(¬q)为假命题,则实数m的取值范围是( )
| A. | (-∞,0)∪(2,+∞) | B. | [0,2] | C. | [2,+∞) | D. | [-2,0] |
20.已知抛物线C:y2=12x的焦点为F,准线为l,P为l上一点,Q是直线PF与抛物线的一个交点,若2$\overrightarrow{FP}$+3$\overrightarrow{FQ}$=$\overrightarrow{0}$,则$\overrightarrow{|QF|}$=( )
| A. | 5 | B. | $\frac{15}{2}$ | C. | 10 | D. | 15 |
7.平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,则|$\overrightarrow{a}$-2$\overrightarrow{b}$|=( )
| A. | $2\sqrt{3}$ | B. | 0 | C. | $\sqrt{6}$ | D. | 2 |
4.以F(1,0)为焦点的抛物线的标准方程是( )
| A. | x=4y2 | B. | y=4x2 | C. | x2=4y | D. | y2=4x |