题目内容
18．已知a=log23，则4a=9．分析 根据对数的定义和指数幂的运算性质计算即可．
解答 解：∵a=log23，
∴2a=3，
∴4a=（2a）2=9，
故答案为：9．
点评 本题考查了对数的定义以及指数幂的运算性质，属于基础题．
练习册系列答案
相关题目
9．
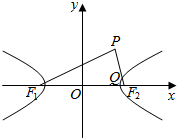如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$，（$\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）
如图，已知F1、F2为双曲线C：$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0）的左、右焦点，点P在第一象限，且满足$\overrightarrow{|{F}_{2}P|}$=$\overrightarrow{a}$，（$\overrightarrow{{F}_{1}P}+\overrightarrow{{F}_{1}{F}_{2}}$）•$\overrightarrow{{F}_{2}P}$=0，线段PF2与双曲线C交于点Q，若$\overrightarrow{{F}_{2}P}$=5$\overrightarrow{{F}_{2}Q}$，则双曲线C的渐近线方程为（ ）| A． | y=±$\frac{\sqrt{5}}{5}x$ | B． | y=±$\frac{1}{2}x$ | C． | y=±$\frac{\sqrt{3}}{2}x$ | D． | y=±$\frac{\sqrt{3}}{3}x$ |
13．已知函数f（x）=$\left\{\begin{array}{l}{{2}^{x}，x＞0}\\{x+1，x≤0}\end{array}\right.$，则f（-2）=（ ）
| A． | -1 | B． | 0 | C． | $\frac{1}{4}$ | D． | 4 |
10．已知命题P：?x∈R，mx2+1＜1；q：?x∈R，x2+mx+1≥0，若p∨（￢q）为假命题，则实数m的取值范围是（ ）
| A． | （-∞，0）∪（2，+∞） | B． | [0，2] | C． | [2，+∞） | D． | [-2，0] |