题目内容
15．
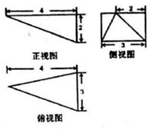某几何体的三视图如图所示，则该几何体中最长的棱长为（ ）| A． | 3$\sqrt{3}$ | B． | 2$\sqrt{6}$ | C． | $\sqrt{21}$ | D． | 2$\sqrt{5}$ |
分析 首先由三视图得到几何体的形状，然后根据图中数据计算最长棱的长度．
解答 
解：由三视图得到几何体为四棱锥P-ABCD，如图其中最长棱长为PA=$\sqrt{P{D}^{2}+A{D}^{2}}=\sqrt{{2}^{2}+{4}^{2}+{2}^{2}}=\sqrt{24}=2\sqrt{6}$；
故选B
点评 本题考查了由几何体的三视图求几何体在最长棱；关键是正确还原几何体．
练习册系列答案
尖子生新课堂课时作业系列答案
相关题目
5．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，$\overrightarrow{a}$-$\overrightarrow{b}$=（$\sqrt{3}$，$\sqrt{2}$），则|2$\overrightarrow{a}$+$\overrightarrow{b}$|=（ ）
| A． | 2$\sqrt{2}$ | B． | $\sqrt{17}$ | C． | $\sqrt{15}$ | D． | 2$\sqrt{5}$ |
6．已知sin（$\frac{3π}{2}$-θ）+3cos（π-θ）=sin（-θ），则sinθcosθ+cos2θ=（ ）
| A． | -$\frac{1}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{5}{17}$ |
3．已知甲，乙两辆车去同一货场装货物，货场每次只能给一辆车装货物，所以若两辆车同时到达，则需要有一车等待．已知甲、乙两车装货物需要的时间都为30分钟，倘若甲、乙两车都在某1小时内到达该货场，则至少有一辆车需要等待装货物的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
10．若对?x∈[1，2]，有x2-a≤0恒成立，则a的取值范围是（ ）
| A． | a≤4 | B． | a≥4 | C． | a≤5 | D． | a≥5 |
20．已知圆x2+y2-4x-6y+9=0与直线y=kx+3相交于A，B两点，若$|{AB}|≥2\sqrt{3}$，则k的取值范围是（ ）
| A． | [-$\frac{3}{4}$，0] | B． | [-$\frac{\sqrt{3}}{3}$，$\frac{\sqrt{3}}{3}$] | C． | [-$\sqrt{3}$，$\sqrt{3}$] | D． | [-$\frac{2}{3}$，0] |