题目内容
在△ABC中,角A,B,C的对边分别为a,b,c,且a<b<c,
a=2bsinA.
(Ⅰ)求角B的大小;
(Ⅱ)若a=2,b=
,求c边的长和△ABC的面积.
| 3 |
(Ⅰ)求角B的大小;
(Ⅱ)若a=2,b=
| 7 |
考点:正弦定理,余弦定理
专题:三角函数的求值
分析:(Ⅰ)已知等式利用正弦定理化简,根据sinA不为0求出sinB的值,即可确定出角B的大小;
(Ⅱ)由a,b,cosB的值,利用余弦定理求出c的值,再由a,c,sinB的值,利用三角形面积公式即可求出△ABC的面积.
(Ⅱ)由a,b,cosB的值,利用余弦定理求出c的值,再由a,c,sinB的值,利用三角形面积公式即可求出△ABC的面积.
解答:
解:(Ⅰ)∵
a=2bsinA,
∴
sinA=2sinAsinB,
∵0<A<π,∴sinA≠0,
∴sinB=
,
∵0<B<π,且a<b<c,
∴B=60°;
(Ⅱ)∵a=2,b=
,cosB=
,
∴由余弦定理得:(
)2=22+c2-2×2×c×
,即c2-2c-3=0,
解得:c=3或c=-1(舍),
∴c=3,
则S△ABC=
acsinB=
×2×3×
=
.
| 3 |
∴
| 3 |
∵0<A<π,∴sinA≠0,
∴sinB=
| ||
| 2 |
∵0<B<π,且a<b<c,
∴B=60°;
(Ⅱ)∵a=2,b=
| 7 |
| 1 |
| 2 |
∴由余弦定理得:(
| 7 |
| 1 |
| 2 |
解得:c=3或c=-1(舍),
∴c=3,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 2 |
点评:此题考查了正弦、余弦定理,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
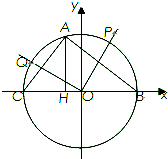 如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧
如图,已知B、C是以原点O为圆心,半径为1的圆与x轴的交点,点A在劣弧 |
| PQ |
| AH |
| AB |
| AC |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
设全集U=R,集合A={x|2x>1},B={x|-1≤x≤5},则(∁UA)∩B等于( )
| A、[-1,0) |
| B、(0,5] |
| C、[-1,0] |
| D、[0,5] |
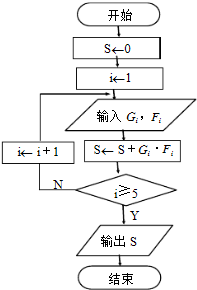 为了了解广东人的生活幸福指数,对40到60岁中年人一天的运动时间(单位:t),现随机地选出50名做调查,下表是一天运动时间频率分布表:
为了了解广东人的生活幸福指数,对40到60岁中年人一天的运动时间(单位:t),现随机地选出50名做调查,下表是一天运动时间频率分布表: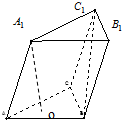 已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示:
已知三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,A1在底面ABC内的射影O为底面△ABC的中心,如图所示: