题目内容
已知a=(2cos x+2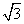 sin x,1),b=(y,cos x),且a∥b.
sin x,1),b=(y,cos x),且a∥b.
(1)将y表示成x的函数f(x),并求f(x)的最小正周期;
(2)记f(x)的最大值为M,a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f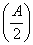 =M,且a=2,求bc的最大值.
=M,且a=2,求bc的最大值.
解析:(1)由a∥b,得2cos2x+2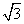 sin xcos x-y=0,
sin xcos x-y=0,
即y=2cos2x+2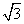 sin xcos x=cos 2x+
sin xcos x=cos 2x+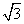 sin 2x+1=2sin
sin 2x+1=2sin +1,
+1,
所以f(x)=2sin +1.又T=
+1.又T= =
= =π,
=π,
所以函数f(x)的最小正周期为π.
(2)由(1)易得M=3,
于是f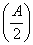 =M=3,即2sin
=M=3,即2sin +1=3⇒sin
+1=3⇒sin =1,因为A为三角形的内角,故A=
=1,因为A为三角形的内角,故A=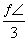 .
.
由余弦定理a2=b2+c2-2bccos A,得4=b2+c2-bc≥2bc-bc=bc,解得bc≤4,于是当且仅当b=c=2时,bc取得最大值,且最大值为4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
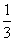
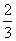 D.
D.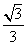
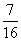 ,且对于任意的n∈N+有Sn,Sn+2,Sn+1成等差数列.
,且对于任意的n∈N+有Sn,Sn+2,Sn+1成等差数列.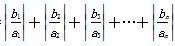 ,若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,求实数m的范围.
,若(n-1)2≤m(Tn-n-1)对于n≥2恒成立,求实数m的范围. 的图象上各点的横坐标伸长到原来的3倍,再向右平移
的图象上各点的横坐标伸长到原来的3倍,再向右平移 个单位,得到的函数的一个对称中心是( )
个单位,得到的函数的一个对称中心是( )
 +ai是实数,则实数a=________.
+ai是实数,则实数a=________.