题目内容


如图，△ABC的角平分线AD的延长线交它的外接圆于点E.

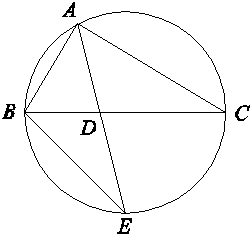
(1)求证：△ABE∽△ADC；

(2)若△ABC的面积S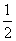＝AD·AE，求∠BAC的大小．


 (1)证明：由已知条件，可得∠BAE＝∠CAD.

因为∠AEB与∠ACB是同弧上的圆周角，

所以∠AEB＝∠ACD.

故△ABE∽△ADC.

(2)因为△ABE∽△ADC，所以＝，

即AB·AC＝AD·AE.

又S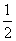＝AB·ACsin ∠BAC，且S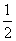＝AD·AE，

故AB·ACsin ∠BAC＝AD·AE.

则sin ∠BAC＝1，

又∠BAC为三角形内角，所以∠BAC＝90°.


练习册系列答案
相关题目

设等比数列{an}的前n项和为Sn，则“a1＞0”是“S3＞S2”的________条件．

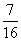已知数列{an}为等比数列，其前n项和为Sn，已知a1＋a4＝－，且对于任意的n∈N＋有Sn，Sn＋2，Sn＋1成等差数列．

(1)求数列{an}的通项公式；

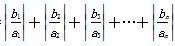(2)已知bn＝n(n∈N＋)，记Tn＝，若(n－1)2≤m(Tn－n－1)对于n≥2恒成立，求实数m的范围．

设函数f(x)＝|x－a|＋3x，其中a＞0.

(1)当a＝1时，求不等式f(x)≥3x＋2的解集；

(2)若不等式f(x)≤0的解集为{x|x≤－1}，求a的值．

设函数f(x)＝1－|2x－3|.

(1)求不等式f(x)≥3x＋1的解集；

(2)若不等式f(x)－mx≥0的解集非空，求m的取值范围．

设(1＋2i) ＝3－4i(i为虚数单位)，则|z|＝________．

设i是虚数单位，若z＝＋ai是实数，则实数a＝________．　

已知平面向量a＝(1，x)，b＝(2x＋3，－x)，x∈R.

(1) 若a⊥b，求x的值；

(2) 若a∥b，求|a－b|的值．

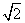已知正方体的棱长为1，其俯视图是一个面积为1的正方形，侧视图是一个面积为的矩形，则该正方体的正视图的面积等于(　　)

A.                            B．1 

C.                         D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网