题目内容
20.若对?x∈R,kx2-kx-1<0是真命题,则k的取值范围是( )| A. | -4≤k≤0 | B. | -4≤k<0 | C. | -4<k≤0 | D. | -4<k<0 |
分析 对k=0与k<0,k>0,分别利用?x∈R,kx2-kx-1<0是真命题,求出k的范围.
解答 解:当k=o时,对?x∈R,kx2-kx-1<0,-1<0即是真命题,成立.
当k<0时,对?x∈R,kx2-kx-1<0是真命题,必有△=(-k)2+4k<0,
解得,-4<k<0,
当k>0时,对?x∈R,kx2-kx-1<0是真命题,显然不成立.
综上,-4<k≤0.
故选:C.
点评 本题考查不等式的解法,恒成立问题,考查转化思想,分类讨论.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.已知双曲线方程为$\frac{x^2}{{{m^2}+4}}-\frac{y^2}{b^2}=1$,若其过焦点的最短弦长为2,则该双曲线的离心率的取值范围是( )
| A. | $(1,\frac{{\sqrt{6}}}{2}]$ | B. | $[\frac{{\sqrt{6}}}{2},+∞)$ | C. | $(1,\frac{{\sqrt{6}}}{2})$ | D. | $(\frac{{\sqrt{6}}}{2},+∞)$ |
15.设函数f'(x)是奇函数f(x)(x∈R)的导函数,f(-2)=0,当x>0时,$f(x)+\frac{x}{3}f'(x)>0$,则使得f(x)>0成立的x的取值范围是( )
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2)∪(-2,2) | D. | (0,2)∪(2,+∞) |
5.在△ABC中,已知∠A=60°,AB:AC=8:5,面积为10$\sqrt{3}$,则AB=( )
| A. | 8 | B. | 6 | C. | 5 | D. | 10 |
12.设等比数列{an}的前n项和为Sn,若a3=4,S3=7,则S6的值为( )
| A. | 31 | B. | 32 | C. | 63 | D. | 64 |
9.若三条直线ax+y+1=0,y=3x,x+y=4,交于一点,则a的值为( )
| A. | 4 | B. | -4 | C. | $\frac{2}{3}$ | D. | -$\frac{2}{3}$ |
10.已知函数f(x)=x3-6x2+9x,g(x)=$\frac{1}{3}$x3-$\frac{a+1}{2}$x2+ax-$\frac{1}{3}$(a>1)若对任意的x1∈[0,4],总存在x2∈[0,4],使得f(x1)=g(x2),则实数a的取值范围为( )
| A. | (1,$\frac{9}{4}$] | B. | [9,+∞) | C. | (1,$\frac{9}{4}$]∪[9,+∞) | D. | [$\frac{3}{2}$,$\frac{9}{4}$]∪[9,+∞) |
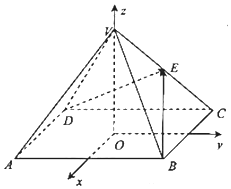 如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.
如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.