题目内容
20.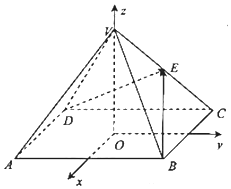 如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.
如图,以正四棱锥V-ABCD的底面中心O为坐标原点建立空间直角坐标系O-xyz,其中Ox∥BC,Oy∥AB,E为VC中点,正四棱锥的底面边长为2a,高为h,且有cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$.(1)求$\frac{h}{a}$的值;
(2)求二面角B-VC-D的余弦值.
分析 (1)由题意求得所用点的坐标,得到向量$\overrightarrow{BE}、\overrightarrow{DE}$的坐标,再由cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$列式求得$\frac{h}{a}$的值;
(2)由(1)得到向量$\overrightarrow{BE}、\overrightarrow{DE}$的坐标,进一步得到$\overrightarrow{CB}、\overrightarrow{CD}$的坐标,求出平面BVC与平面DVC的一个法向量,求出两法向量所成角的余弦值,可得二面角B-VC-D的余弦值.
解答 解:(1)由题意,可得B(a,a,0),C(-a,a,0),D(-a,-a,0),V(0,0,h),E($-\frac{a}{2},\frac{a}{2},\frac{h}{2}$),
∴$\overrightarrow{BE}=(-\frac{3a}{2},-\frac{a}{2},\frac{h}{2})$,$\overrightarrow{DE}=(\frac{a}{2},\frac{3a}{2},\frac{h}{2})$.
故cos<$\overrightarrow{BE},\overrightarrow{DE}$>=$\frac{{h}^{2}-6{a}^{2}}{{h}^{2}+10{a}^{2}}$,
又cos<$\overrightarrow{BE}$,$\overrightarrow{DE}$>=-$\frac{15}{49}$,∴$\frac{{h}^{2}-6{a}^{2}}{{h}^{2}+10{a}^{2}}=-\frac{15}{49}$,解得:$\frac{h}{a}=\frac{3}{2}$;
(2)由$\frac{h}{a}=\frac{3}{2}$,得$\overrightarrow{BE}=(-\frac{3a}{2},-\frac{a}{2},\frac{3a}{4})$,$\overrightarrow{DE}=(\frac{a}{2},\frac{3a}{2},\frac{3a}{4})$.
且$\overrightarrow{CB}=(2a,0,0),\overrightarrow{DC}=(0,2a,0)$.
设平面BVC的一个法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,则$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{BE}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{CB}=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{-\frac{3a}{2}{x}_{1}-\frac{a}{2}{y}_{1}+\frac{3a}{4}{z}_{1}=0}\\{2a{x}_{1}=0}\end{array}\right.$,取y1=3,得$\overrightarrow{{n}_{1}}=(0,3,2)$;
同理可得平面DVC的一个法向量$\overrightarrow{{n}_{2}}=(-3,0,2)$.
∴cos<$\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}$>=$\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}$=$\frac{0×(-3)+3×0+2×2}{\sqrt{13}×\sqrt{13}}=\frac{4}{13}$.
∴二面角B-VC-D的余弦值为-$\frac{4}{13}$.
点评 本题考查二面角的平面角及其求法,考查空间想象能力和思维能力,考查计算能力,属中档题.

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
| A. | $\frac{9}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{8}$ |
| A. | 0°≤α<180° | B. | 45°≤α<180° | ||
| C. | 0°≤α≤45°或90°<α<180° | D. | 0°≤α≤45°或90°≤α<180° |
| A. | -4≤k≤0 | B. | -4≤k<0 | C. | -4<k≤0 | D. | -4<k<0 |