题目内容

12．设等比数列{an}的前n项和为Sn，若a3=4，S3=7，则S6的值为（　　）
A．31B．32C．63D．64

分析 根据比数列通项公式和前n项和公式进行计算即可．

解答 解：设等比数列的公式为q，则${a}_{1}{q}^{2}=4$，$\frac{{a}_{1}（1-{q}^{3}）}{1-q}=7$，
解得：a1=1，q=2，
那么：${S}_{6}=\frac{{a}_{1}（1-{q}^{6}）}{1-q}=\frac{1-{2}^{6}}{1-2}=63$．
故选C．

点评 本题主要考查等比数列通项公式和前n项和公式的应用．

练习册系列答案
相关题目
11．设F1，F2分别为椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1（{a_1}＞{b_1}＞0）$与双曲线C2：$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1（{a_2}＞0，{b_2}＞0）$的公共焦点，它们在第一象限内交于点M，∠F1MF2=90°，若椭圆的离心率${e_1}=\frac{3}{4}$，则双曲线C2的离心率e2的值为（　　）
A．$\frac{9}{2}$B．$\frac{{3\sqrt{2}}}{2}$C．$\frac{3}{2}$D．$\frac{5}{4}$
3．过点M（0，1）和N（-1，m2）（m∈R）的直线的倾斜角α的取值范围是（　　）
A．0°≤α＜180°B．45°≤α＜180°
C．0°≤α≤45°或90°＜α＜180°D．0°≤α≤45°或90°≤α＜180°
20．若对?x∈R，kx2-kx-1＜0是真命题，则k的取值范围是（　　）
A．-4≤k≤0B．-4≤k＜0C．-4＜k≤0D．-4＜k＜0
7．在单调递增的等比数列{an}中，a1•a9=64，a3+a7=20，求a11=64．
17．已知双曲线的左、右焦点分别是F1，F2，过F2的直线交双曲线的右支于P，Q两点，若|PF2|=|F1F2|，且|QF2|=2|PF2|，则该双曲线的离心率为（　　）
A．$\frac{4}{3}$B．$\frac{5}{3}$C．$\frac{7}{5}$D．$\frac{8}{5}$
4．各项均为正数的数列{an}中，a1=1，Sn是数列{an}的前n项和，对任意n∈N+，6Sn=an2+3an+2．
（1）求数列{an}的通项公式；
（2）记bn=$\frac{1}{{a}_{n}•{a}_{n+1}}$，求数列{bn}的前n项和Tn．
1．若函数f（x）=$\frac{{2}^{x+1}}{{2}^{x}+1}$，则f（-$\frac{1}{3}$）+f（-$\frac{1}{2}$）+f（-1）+f（0）+f（1）+f（$\frac{1}{2}$）+f（$\frac{1}{3}$）=7．
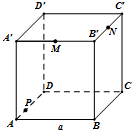2．如图，在棱长为a的正方体ABCD-A′B′C′D′中，M、N分别是棱A′B′、B′C′的中点，P是棱AD上一点，AP=$\frac{a}{3}$，过P、M、N的平面与棱CD交于Q，则PQ的长度为$\frac{2\sqrt{\sqrt{2}}}{3}$a．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网