题目内容
5.在△ABC中,已知∠A=60°,AB:AC=8:5,面积为10$\sqrt{3}$,则AB=( )| A. | 8 | B. | 6 | C. | 5 | D. | 10 |
分析 由已知可得:AC=$\frac{5}{8}$AB,进而利用三角形面积公式即可计算得解AB的值.
解答 解:∵AB:AC=8:5,可得:AC=$\frac{5}{8}$AB,
又∵∠A=60°,面积为10$\sqrt{3}$=$\frac{1}{2}$AB•AC•sinA=$\frac{1}{2}×$AB×$\frac{5}{8}$AB×$\frac{\sqrt{3}}{2}$,
∴解得:AB=8.
故选:A.
点评 本题主要考查了三角形面积公式在解三角形中的应用,考查了计算能力,属于基础题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
13.高二某班共有学生60人,座号分别为1,2,3,…,60现根据座号,用系统抽样的方法,抽取一个容量为5的样本.已知4号、28号、40号、52号同学在样本中,那么样本中还有一个同学的座号是( )
| A. | 14 | B. | 16 | C. | 36 | D. | 56 |
20.若对?x∈R,kx2-kx-1<0是真命题,则k的取值范围是( )
| A. | -4≤k≤0 | B. | -4≤k<0 | C. | -4<k≤0 | D. | -4<k<0 |
10.如果a<b<0,则下列不等式成立的是( )
| A. | $\frac{1}{a}$<$\frac{1}{b}$ | B. | a-c<b-c | C. | ac2<bc2 | D. | a2<b2 |
17.已知双曲线的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF2|=|F1F2|,且|QF2|=2|PF2|,则该双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{5}$ | D. | $\frac{8}{5}$ |
14.已知函数f(x)=$\frac{\sqrt{5-ax}}{a-2}$(a∈A),若f(x)在区间(0,1]上是减函数,则集合A可以是( )
| A. | (-∞,0) | B. | [1,2) | C. | (-1,5] | D. | [4,6] |
15.当x>0时,f(x)=$\frac{12}{x}$+4x的最小值为( )
| A. | 8$\sqrt{3}$ | B. | 8 | C. | 16 | D. | 4 |
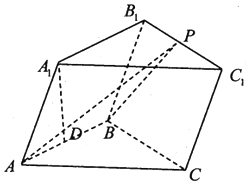 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.