题目内容
19.已知双曲线方程为$\frac{x^2}{{{m^2}+4}}-\frac{y^2}{b^2}=1$,若其过焦点的最短弦长为2,则该双曲线的离心率的取值范围是( )| A. | $(1,\frac{{\sqrt{6}}}{2}]$ | B. | $[\frac{{\sqrt{6}}}{2},+∞)$ | C. | $(1,\frac{{\sqrt{6}}}{2})$ | D. | $(\frac{{\sqrt{6}}}{2},+∞)$ |
分析 由题意,通径为$\frac{2{b}^{2}}{a}$=2,a≥2,可得b=$\sqrt{a}$,利用e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{1}{a}}$≤$\frac{\sqrt{6}}{2}$,e>1,即可得出结论.
解答 解:由题意,$\frac{2{b}^{2}}{a}$=2,a≥2
∴b=$\sqrt{a}$,
∴e=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{1+\frac{1}{a}}$≤$\frac{\sqrt{6}}{2}$,
∵e>1,
∴1<e≤$\frac{\sqrt{6}}{2}$,
故选A.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
10.若抛物线y2=2px的准线经过双曲线x2-y2=2的右焦点,则p的值为( )
| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
11.设F1,F2分别为椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1({a_1}>{b_1}>0)$与双曲线C2:$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1({a_2}>0,{b_2}>0)$的公共焦点,它们在第一象限内交于点M,∠F1MF2=90°,若椭圆的离心率${e_1}=\frac{3}{4}$,则双曲线C2的离心率e2的值为( )
| A. | $\frac{9}{2}$ | B. | $\frac{{3\sqrt{2}}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{4}$ |
8.某个路口交通指示灯,红灯时间为30秒,黄灯时间为10秒,绿灯时间为40秒,黄灯时间可以通行,当你到达路口时,等待时间不超过10秒就可以通行的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{8}$ |
20.若对?x∈R,kx2-kx-1<0是真命题,则k的取值范围是( )
| A. | -4≤k≤0 | B. | -4≤k<0 | C. | -4<k≤0 | D. | -4<k<0 |
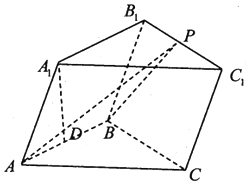 在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.
在三棱柱ABC-A1B1C1中,已知侧面ABB1A1是菱形,侧面BCC1B1是正方形,点A1在底面ABC的投影为AB的中点D.