题目内容
8.已知函数f(x)=$\frac{{a}^{x}-1}{{a}^{x}+1}$(a>0,a≠1).(1)求f(x)的定义域,值域;
(2)讨论函数f(x)的单调性,并加以证明.
分析 (1)定义域易得,利用反解自变量的方法求值域即可.
(2)先把函数分离常数,在分底数和1的大小两种情况再结合复合函数的单调性来判断即可.
解答 解:(1)易得f(x)的定义域为{x|x∈R}.
设y=$\frac{{a}^{x}-1}{{a}^{x}+1}$,解得ax=-$\frac{y+1}{y-1}$①
∵ax>0当且仅当-$\frac{y+1}{y-1}$>0时,方程①有解.解-$\frac{y+1}{y-1}$>0得-1<y<1.
∴f(x)的值域为{y|-1<y<1}.
(2)f(x)=1-$\frac{2}{{a}^{x}+1}$,
1°当a>1时,∵ax+1为增函数,且ax+1>0,
∴$\frac{2}{{a}^{x}+1}$为减函数,从而f(x)为增函数,
2°当0<a<1时,类似地可得f(x)为减函数;
证明如下:
设x1<x2,
则f(x1)-f(x2)=1-$\frac{2}{{a}^{{x}_{1}}+1}$-1+$\frac{2}{{a}^{{x}_{2}}+1}$=$\frac{2{(a}^{{x}_{1}}{-a}^{{x}_{2}})}{{(a}^{{x}_{1}}+1){(a}^{{x}_{2}}+1)}$,
0<a<1时,由x1<x2,得:${a}^{{x}_{1}}$>${x}^{{x}_{2}}$,
故f(x1)>f(x2),f(x)是减函数,
a>1时,由x1<x2,得:${a}^{{x}_{1}}$<${x}^{{x}_{2}}$,
故f(x1)<f(x2),f(x)是增函数.
点评 本题是对函数定义域和值域以及单调性的综合考查.在利用复合函数的单调性时,其原则是;单调性相同为增,单调性相反为减,且乘正数单调性不变,乘负数单调性相反.

练习册系列答案
相关题目
8.某个路口交通指示灯,红灯时间为30秒,黄灯时间为10秒,绿灯时间为40秒,黄灯时间可以通行,当你到达路口时,等待时间不超过10秒就可以通行的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{7}$ | C. | $\frac{5}{7}$ | D. | $\frac{5}{8}$ |
3.过点M(0,1)和N(-1,m2)(m∈R)的直线的倾斜角α的取值范围是( )
| A. | 0°≤α<180° | B. | 45°≤α<180° | ||
| C. | 0°≤α≤45°或90°<α<180° | D. | 0°≤α≤45°或90°≤α<180° |
13.高二某班共有学生60人,座号分别为1,2,3,…,60现根据座号,用系统抽样的方法,抽取一个容量为5的样本.已知4号、28号、40号、52号同学在样本中,那么样本中还有一个同学的座号是( )
| A. | 14 | B. | 16 | C. | 36 | D. | 56 |
20.若对?x∈R,kx2-kx-1<0是真命题,则k的取值范围是( )
| A. | -4≤k≤0 | B. | -4≤k<0 | C. | -4<k≤0 | D. | -4<k<0 |
17.已知双曲线的左、右焦点分别是F1,F2,过F2的直线交双曲线的右支于P,Q两点,若|PF2|=|F1F2|,且|QF2|=2|PF2|,则该双曲线的离心率为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{7}{5}$ | D. | $\frac{8}{5}$ |
18.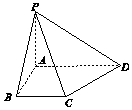 四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )
四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )
 四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )
四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,BC∥AD,且AB=BC=2,AD=3,PA⊥平面ABCD且PA=2,则PB与平面PCD所成角的正弦值为( )| A. | $\frac{\sqrt{42}}{7}$ | B. | $\frac{\sqrt{7}}{7}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |