题目内容
已知等差数列{an}的前n项和为Sn,且S4=16,S6=36.
(1)求an;
(2)设数列{bn}满足bn=qan(q∈R,q>0),Tn=
+
+…+
,求Tn.
(1)求an;
(2)设数列{bn}满足bn=qan(q∈R,q>0),Tn=
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的公差为d,由S4=16,S6=36.利用等差数列的通项公式及其前n项和公式即可得出.
(Ⅱ)bn=qan=q2n-1,利用等比数列的通项公式及其前n项和公式即可得出.
(Ⅱ)bn=qan=q2n-1,利用等比数列的通项公式及其前n项和公式即可得出.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,由S4=16,S6=36.
可得
,
解得
,
∴an=1+2(n-1)=2n-1.
(Ⅱ)bn=qan=q2n-1,
∴数列{
}是首项为
,公比为
的等比数列,
当q≠1时,
Tn=
+
+…+
=
=
(1-
),
当q=1时,Tn=n.
∴Tn=
.
可得
|
解得
|
∴an=1+2(n-1)=2n-1.
(Ⅱ)bn=qan=q2n-1,
∴数列{
| 1 |
| bnbn+1 |
| 1 |
| q4 |
| 1 |
| q4 |
当q≠1时,
Tn=
| 1 |
| b1b2 |
| 1 |
| b2b3 |
| 1 |
| bnbn+1 |
| ||||
1-
|
| 1 |
| q4-1 |
| 1 |
| q4n |
当q=1时,Tn=n.
∴Tn=
|
点评:本题考查了等比数列与等差数列的通项公式及前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
已知cosα=
,cos(α+β)=-
,且α、β∈(0,
),则cos(α-β)=( )
| 1 |
| 3 |
| 1 |
| 3 |
| π |
| 2 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知三棱锥P-ABC,PA⊥面ABC,∠ABC=90°,PA=2,AB=
,BC=1,则该三棱锥的外接球体积为( )
| 3 |
| A、8π | ||||
B、
| ||||
C、
| ||||
D、12
|
函数f(x)=log2|2x-1|的图象大致是( )
A、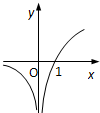 |
B、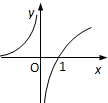 |
C、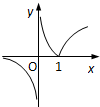 |
D、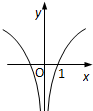 |