题目内容
已知数列{an}中,a2=1,前n项和为Sn,且Sn=
(n∈N*).
(1)求数列{an}的通项公式;
(2)求
的值.
| n(an-a1) |
| 2 |
(1)求数列{an}的通项公式;
(2)求
| lim |
| n→∞ |
| Sn |
| n2 |
考点:数列的求和,极限及其运算
专题:等差数列与等比数列
分析:(1)当n=1时,a1=S1=
,可得a1=0.Sn=
an.当n≥3时,an=Sn-Sn-1,化为
=
,利用“累乘求积”即可得出.
(2)利用等差数列的前n项和公式可得Sn,再利用数列的运算法则即可得出.
| a1-a1 |
| 2 |
| n |
| 2 |
| an |
| an-1 |
| n-1 |
| n-2 |
(2)利用等差数列的前n项和公式可得Sn,再利用数列的运算法则即可得出.
解答:
解:(1)当n=1时,a1=S1=
,可得a1=0.
∴Sn=
an.
当n≥3时,an=Sn-Sn-1=
-
,
化为
=
,
∴an=
•
•…•
•
•a2
=
•
•…•
•1
=n-1.
当n=1,2时也成立,
∴an=n-1(n∈N*).
(2)由(1)可得:Sn=
=
.
∴
=
=
.
| a1-a1 |
| 2 |
∴Sn=
| n |
| 2 |
当n≥3时,an=Sn-Sn-1=
| nan |
| 2 |
| (n-1)an-1 |
| 2 |
化为
| an |
| an-1 |
| n-1 |
| n-2 |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a4 |
| a3 |
| a3 |
| a2 |
=
| n-1 |
| n-2 |
| n-2 |
| n-3 |
| 2 |
| 1 |
=n-1.
当n=1,2时也成立,
∴an=n-1(n∈N*).
(2)由(1)可得:Sn=
| n(n-1+0) |
| 2 |
| n(n-1) |
| 2 |
∴
| lim |
| n→∞ |
| Sn |
| n2 |
| lim |
| n→∞ |
| n-1 |
| 2n |
| 1 |
| 2 |
点评:本题考查了“累乘求积”方法、等差数列的前n项和公式、数列的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若方程ln(x+1)+2x-1=0的根为x=m,则( )
| A、0<m<1 |
| B、1<m<2 |
| C、2<m<3 |
| D、3<m<4 |
 已知点P(x,y)在如图所示的正六边形P1P2P3P4P5P6区域(含边界)内运动,则当z=4x+5y取到最大值时,点P为于( )
已知点P(x,y)在如图所示的正六边形P1P2P3P4P5P6区域(含边界)内运动,则当z=4x+5y取到最大值时,点P为于( )| A、P1 |
| B、P2 |
| C、P3 |
| D、P4 |
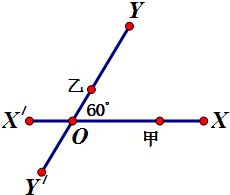 如图,有两条相交成60°角的直路XX′,YY′,交点为O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后来甲沿XX′的方向,乙沿Y′Y的方向,同时以4km/h的速度步行.
如图,有两条相交成60°角的直路XX′,YY′,交点为O,甲、乙分别在OX,OY上,起初甲离O点3km,乙离O点1km,后来甲沿XX′的方向,乙沿Y′Y的方向,同时以4km/h的速度步行.