题目内容
在Rt△ABC中,CA=CB=3,M,N是斜边AB上的两个动点,且MN=
,则
•
的取值范围为( )
| 2 |
| CM |
| CN |
| A、[3,6] | ||
| B、[4,6] | ||
C、[2,
| ||
| D、[2,4] |
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:通过建立直角坐标系求出AB所在直线的方程,设出M,N的坐标,将
•
=2(b-1)2+4,0≤b≤2,求出范围即可.
| CM |
| CN |
解答:
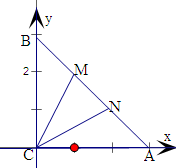 解:以C为坐标原点,CA为x轴建立平面坐标系,
解:以C为坐标原点,CA为x轴建立平面坐标系,
则A(3,0),B(0,3),
∴AB所在直线的方程为:
+
=1,则y=3-x,
设N(a,3-a),M(b,3-b),且0≤a≤3,0≤b≤3不妨设a>b,
∵MN=
,
∴(a-b)2+(b-a)2=2,
∴a-b=1,∴a=b+1,
∴0≤b≤2,
∴
•
=(a,3-a)•(b,3-b)
=2ab-3(a+b)+9,
=2(b2-2b+3)=2(b-1)2+4,0≤b≤2,
∴当b=0或b=2时有最大值6;
当b=1时有最小值4.
∴
•
的取值范围为[4,6]
故选B.
 解:以C为坐标原点,CA为x轴建立平面坐标系,
解:以C为坐标原点,CA为x轴建立平面坐标系,则A(3,0),B(0,3),
∴AB所在直线的方程为:
| x |
| 3 |
| y |
| 3 |
设N(a,3-a),M(b,3-b),且0≤a≤3,0≤b≤3不妨设a>b,
∵MN=
| 2 |
∴(a-b)2+(b-a)2=2,
∴a-b=1,∴a=b+1,
∴0≤b≤2,
∴
| CM |
| CN |
=2ab-3(a+b)+9,
=2(b2-2b+3)=2(b-1)2+4,0≤b≤2,
∴当b=0或b=2时有最大值6;
当b=1时有最小值4.
∴
| CM |
| CN |
故选B.
点评:熟练掌握通过建立直角坐标系、数量积的坐标运算是解题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
在△ABC中,|
|=3,|
|=2,点D满足2
=3
,∠BAC=60°,则
•
=( )
| AB |
| AC |
| BD |
| DC |
| AD |
| BC |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
若x∈[-1,1],则方程2-|x|=sin2πx的实数根的个数为( )
| A、2 | B、3 | C、4 | D、5 |
某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy的最大值为( )
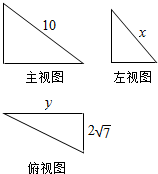

| A、32 | ||
B、32
| ||
| C、64 | ||
D、64
|
已知向量
=(3,1),
=(-2,5),那么2
+
等于( )
| a |
| b |
| a |
| b |
| A、.(-1,11) |
| B、.(4,7) |
| C、.(1,6) |
| D、(5,-4) |
已知函数f(x)=sin(x+
),其中x∈[-
,a],若f(x)的值域是[-
,1],则实数a的取值范围是( )
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|