题目内容
已知曲线C1的参数方程为
(θ为参数),曲线C2的极坐标方程为ρ=2cosθ+6sinθ,问曲线C1,C2是否相交,若相交请求出公共弦的方程,若不相交,请说明理由.
|
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:首先将两个曲线方程化为普通方程,然后由普通方程得到 曲线为圆,由圆心距与半径的关系判定圆的位置关系,两圆的方程相减得到公共弦的方程.
解答:
解:由参数方程为
(θ为参数),消去θ,得曲线C1的普通方程(x+2)2+y2=10①
由ρ=2cosθ+6sinθ,得ρ2=2ρcosθ+6ρsinθ,
∴曲线C2是的普通方程为(x-1)2+(y-3)2=10②
所以曲线C1,C2是圆,并且圆心分别为(-2,0),(1,3),
∴|C1C2|=
=3
<2
,
∴两圆相交,相交时公共弦的方程为①-②得x+y=1.
|
由ρ=2cosθ+6sinθ,得ρ2=2ρcosθ+6ρsinθ,
∴曲线C2是的普通方程为(x-1)2+(y-3)2=10②
所以曲线C1,C2是圆,并且圆心分别为(-2,0),(1,3),
∴|C1C2|=
| (-2-1)2+(0-3)2 |
| 2 |
| 10 |
∴两圆相交,相交时公共弦的方程为①-②得x+y=1.
点评:本题考查了参数方程化为普通方程,以及两圆的公共弦所在的直线方程求法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在二项式(2x+1)6的展开式中,系数最大项的系数是( )
| A、20 | B、160 |
| C、240 | D、192 |
在△ABC中,|
|=3,|
|=2,点D满足2
=3
,∠BAC=60°,则
•
=( )
| AB |
| AC |
| BD |
| DC |
| AD |
| BC |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
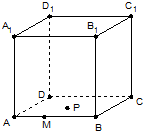 如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=
如图,正方体ABCD-A1B1C1D1的棱长为1,点M在棱AB上,且PB,点AM=| 1 |
| 3 |
| A、圆 | B、抛物线 | C、双曲线 | D、椭圆 |
已知平面α∥平面β,直线m?平面α,那么直线m与平面β 的关系是( )
| A、直线m在平面β内 |
| B、直线m与平面β相交但不垂直 |
| C、直线m与平面β垂直 |
| D、直线m与平面β平行 |
某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy的最大值为( )
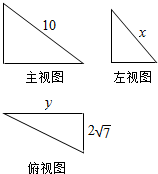

| A、32 | ||
B、32
| ||
| C、64 | ||
D、64
|