题目内容
已知椭圆
+
=1(a>b>0,c为半焦距)的左焦点为F,右顶点为A,抛物线y2=
(a+c)x于椭圆交于B,C两点,若四边形ABFC是平行四边形,则椭圆的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| 15 |
| 8 |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由椭圆方程求出F和A的坐标,由对称性设出B、C的坐标,根据平行四边形的性质求出横坐标,代入抛物线方程求出B的纵坐标,将点B的坐标代入椭圆方程,化简整理得到关于椭圆离心率e的方程,即可得到该椭圆的离心率.
解答:
解:由题意得,椭圆
+
=1(a>b>0,c为半焦距)的左焦点为F,右顶点为A,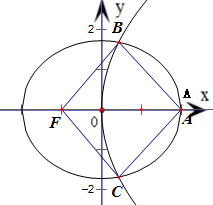
则A(a,0),F(-c,0),
∵抛物线y2=
(a+c)x于椭圆交于B,C两点,
∴B、C两点关于x轴对称,可设B(m,n),C(m,-n)
∵四边形ABFC是平行四边形,∴2m=a-c,则m=
(a-c),
将B(m,n)代入抛物线方程得,n2=
(a+c)m=
(a+c)(a-c)=
(a2-c2),
∴n2=
b2,则不妨设B(
(a-c),
b),再代入椭圆方程得,
+
=1,
化简得
=
,即4e2-8e+3=0,解得e=
或
>1(舍去),
故选:A.
| x2 |
| a2 |
| y2 |
| b2 |

则A(a,0),F(-c,0),
∵抛物线y2=
| 15 |
| 8 |
∴B、C两点关于x轴对称,可设B(m,n),C(m,-n)
∵四边形ABFC是平行四边形,∴2m=a-c,则m=
| 1 |
| 2 |
将B(m,n)代入抛物线方程得,n2=
| 15 |
| 8 |
| 15 |
| 16 |
| 15 |
| 16 |
∴n2=
| 15 |
| 16 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| a2 |
| 15b2 |
| 16b2 |
化简得
| ||
| a2 |
| 1 |
| 16 |
| 1 |
| 2 |
| 3 |
| 2 |
故选:A.
点评:本题考查椭圆、抛物线的标准方程,以及它们的简单几何性质,平行四边形的性质,主要考查了椭圆的离心率e,属于中档题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
把函数y=sin(2x-
)的图象向左平移
个单位后,所得函数图象的一条对称轴为( )
| π |
| 6 |
| π |
| 6 |
| A、x=0 | ||
B、x=
| ||
C、x=-
| ||
D、x=
|
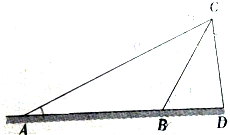 为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为
为了测量一个塔的高度,某人站在A处测得塔尖C的仰角为30°,前进100m后达到B处,测得塔尖的仰角为75°,则该塔的高度为