题目内容
在△ABC中,已知2
asinB=3b且cosB=cosC,A为锐角,则△ABC的形状为( )
| 3 |
| A、等边三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |
考点:余弦定理
专题:解三角形
分析:由条件利用正弦定理可得 3sinB=2
sinAsinB,且 B=C,化简可得sinA=
,由此可得A=
,从而判断△ABC的形状.
| 3 |
| π |
| 3 |
| π |
| 3 |
解答:
解:在△ABC中,2
asinB=3b且cosB=cosC
,则有 3sinB=2
sinAsinB,且 B=C,
解得sinA=
,∴A=
∵A为锐角
∴A=
当A=
时,再由B=C可得△ABC是等边三角形.
故选:A.
| 3 |
,则有 3sinB=2
| 3 |
解得sinA=
| ||
| 2 |
| π |
| 3 |
∵A为锐角
∴A=
| π |
| 3 |
当A=
| π |
| 3 |
故选:A.
点评:本题主要考查正弦定理的应用,判断三角形的形状,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
函数y=lg(-x2-3x+4)的定义域是( )
| A、(-4,-1) |
| B、(-4,1) |
| C、(-1,4) |
| D、[-4,1] |
已知x+1是5和7的等差中项,则x的值为( )
| A、5 | B、6 | C、8 | D、9 |
等差数列{an}中,a1+a4+a7=39,a2+a5+a8=33,则a6的值为( )
| A、10 | B、9 | C、8 | D、7 |
已知向量
=(an,-1),
=(2,an+1),n∈N*且a1=2,
⊥
,则数列{an}的前n项和为Sn=( )
| a |
| b |
| a |
| b |
| A、2n+1-2 |
| B、2-2n+1 |
| C、2n+1 |
| D、3n-1 |
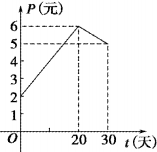 某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示:
某上市股票在30填内每股交易价格P(元)与时间t(天)组成有序数对(t,P),点(t,P)落在图中的两条线段上,该股票在30填内的日交易量Q(万股)与时间t(天)的部分数据如表所示: