题目内容
14.函数y=cos($\frac{π}{4}$-2x)的单调递减区间是( )| A. | [$\frac{π}{8}$+2kπ,$\frac{5π}{8}$+2kπ](k∈Z) | B. | [$\frac{π}{8}$+kπ,$\frac{5π}{8}$+kπ](k∈Z) | ||
| C. | [-$\frac{3π}{8}$+2kπ,$\frac{π}{8}$+2kπ](k∈Z) | D. | [-$\frac{3π}{8}$+kπ,$\frac{π}{8}$+kπ](k∈Z) |
分析 先利用诱导公式将函数解析式化为y=cos(2x-$\frac{π}{4}$),结合余弦函数的单调性,结合2x-$\frac{π}{4}$∈[2kπ,π+2kπ],k∈Z,可得原函数的单调递减区间.
解答 解:函数y=cos($\frac{π}{4}$-2x)=cos(2x-$\frac{π}{4}$),
由2x-$\frac{π}{4}$∈[2kπ,π+2kπ],k∈Z得:
x∈[$\frac{π}{8}$+kπ,$\frac{5π}{8}$+kπ],k∈Z,
即函数y=cos($\frac{π}{4}$-2x)的单调递减区间是[$\frac{π}{8}$+kπ,$\frac{5π}{8}$+kπ],k∈Z,
故选:B.
点评 本题考查的知识点是余弦函数的图象和性质,熟练掌握余弦函数的图象和性质,是解答的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
4.若实数x,y满足不等式组$\left\{\begin{array}{l}x+y≤1\\ x-y≤1\\ x≥0\end{array}\right.$,则2x+y的最大值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
5.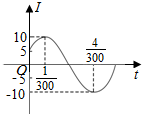 电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
 电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )
电流强度I(安)随时间t(秒)变化的函数I=Asin(ωt+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如右图所示,则当t=$\frac{1}{100}$秒时,电流强度是( )| A. | -5 A | B. | 5A | C. | 5$\sqrt{3}$ A | D. | 10 A |
9.已知M={y∈R|y=x2},N={x∈R|x2+y2=2},则M∩N=( )
| A. | {(-1,1),(1,1)} | B. | {1} | C. | [0,1] | D. | $[{0,\sqrt{2}}]$ |
6.已知抛物线M:y2=4x,圆N:(x-1)2+y2=r2(其中r为常数,r>0).过点(1,0)的直线l交圆N于C、D两点,交抛物线M于A、B两点,且满足|AC|=|BD|的直线l只有三条,则( )
| A. | r∈(0,1] | B. | r∈(1,$\frac{3}{2}$] | C. | r∈($\frac{3}{2}$,2] | D. | r∈(2,+∞) |
4.某场排球赛决赛将在甲队与乙队之间展开,据以往统计,甲队在每局比赛中胜乙队的概率为$\frac{2}{3}$,比赛采取五局三胜制,即谁先胜三局谁就获胜,并停止比赛,则甲队以3:1获胜的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{8}{27}$ | C. | $\frac{2}{9}$ | D. | $\frac{8}{9}$ |