题目内容
14.为振兴苏区发展,赣州市2016年计划投入专项资金加强红色文化基础设施改造.据调查,改造后预计该市在一个月内(以30天记),红色文化旅游人数f(x)(万人)与日期x(日)的函数关系近似满足:$f(x)=3-\frac{1}{20}x$,人均消费g(x)(元)与日期x(日)的函数关系近似满足:g(x)=60-|x-20|.(1)求该市旅游日收入p(x)(万元)与日期x(1≤x≤30,x∈N*)的函数关系式;
(2)当x取何值时,该市旅游日收入p(x)最大.
分析 (1)根据条件建立函数关系即可得到结论.
(2)根据分段函数的表达式,判断函数的单调性即可求出函数的最值.
解答 解:(1)$g(x)=\left\{\begin{array}{l}40+x(1≤x<20,x∈N)\\ 80-x(20≤x≤30,x∈N)\end{array}\right.$(3分)
p(x)=f(x)•g(x),
$p(x)=\left\{\begin{array}{l}-\frac{1}{20}{x^2}+x+120(1≤x<20,x∈N)\\ \frac{1}{20}{x^2}-7x+240(20≤x≤30,x∈N)\end{array}\right.$(6分)
(2)由(1)可知,p(x)在[1,10]上为增函数,在[10,20)上为减函数(8分)
当x∈[1,20)时,p(x)max=p(10)=125(9分)
因为p(x)在[20,30]上为减函数,
所以当x∈[20,30]时,p(x)max=p(20)=120(10分)
综上所述,当x=10时p(x)max=125(12分)
点评 本题主要考查函数的应用问题,根据条件建立函数关系,利用分段函数的表达式判断函数的单调性的性质是解决本题的关键.

练习册系列答案
相关题目
4.过焦点在x轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{16}$=1的右焦点F2的直线交椭圆于A,B两点,F1是椭圆的左焦点,若△AF1B的周长为20,则实数m的值为( )
| A. | 5 | B. | 25 | C. | 10 | D. | 100 |
5.已知集合A={x|1≤x≤3},B={x|0<x<a},若A⊆B,则实数a的范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | [-∞,3] | D. | [-∞,3) |
2.已知$sin(-\frac{3}{2}π+θ)=\frac{1}{5}$,则cosθ=( )
| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $-\frac{2}{5}$ |
9.已知$cos(\frac{π}{4}+θ)=\frac{2}{3}\sqrt{2}$,则sin2θ=( )
| A. | $-\frac{7}{9}$ | B. | $\frac{7}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{8}{9}$ |
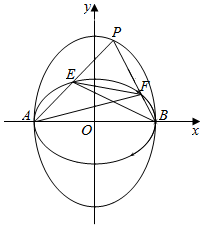 椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.
椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.