题目内容
4.若椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1上一点P到焦点F1(-2,0)的距离为$\frac{13}{3}$,则△PF1F2的面积为$\frac{4}{3}$.分析 设出P(m,n),代入椭圆方程,求得椭圆的a,b,c,e,运用椭圆的焦半径公式解方程可得m=2,求得n,再由三角形的面积公式,计算即可得到.
解答 解:设P(m,n),则$\frac{{m}^{2}}{9}$+$\frac{{n}^{2}}{5}$=1,
椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的a=3,b=$\sqrt{5}$,c=$\sqrt{9-5}$=2,e=$\frac{c}{a}$=$\frac{2}{3}$,
由椭圆的焦半径公式可得,
|PF1|=a+em=3+$\frac{2}{3}$m=$\frac{13}{3}$,
解得m=2,n=±$\frac{5}{3}$,
则△PF1F2的面积为$\frac{1}{2}$|F1F2|•|n|=2•$\frac{2}{3}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查椭圆的方程和性质,考查焦点三角形的面积的求法,注意运用焦半径公式,属于中档题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
15.若直线l1:ax+2y+6=0与直线l2:x+(a-1)y-1=0垂直,则实数a=( )
| A. | $\frac{2}{3}$ | B. | -1 | C. | 2 | D. | -1或2 |
12.已知椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,直线l与椭圆交于与椭圆相交于A、B两点,点P(1,1)是线段AB的中点,则直线l的斜率为( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{3}{4}$ | D. | $\frac{3}{4}$ |
13.抛物线y=$\frac{{x}^{2}}{4}$的焦点为F,点P在抛物线上,若|PF|=5,则点P到y轴的距离为( )
| A. | 6 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 4 |
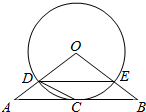 如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.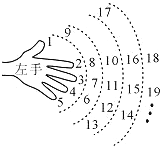 如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).
如图,一个小朋友按如图所示的规则练习数数,1大拇指,2食指,3中指,4无名指,5小指,6无名指,…,一直数到2015时,对应的指头是中指(填指头的名称).
