题目内容
6.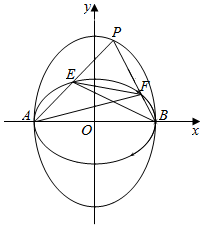 椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.
椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.(Ⅰ)求椭圆C1与C2的方程;
(Ⅱ)设P是椭圆C2上非顶点的动点,P与椭圆C1长轴两个顶点A,B的连线PA,PB分别与椭圆C1交于点E,F.
(1)求证:直线PA,PB斜率之积为常数;
(2)直线AF与直线BE的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
分析 (Ⅰ)依题意$e=\frac{{\sqrt{2}}}{2}$,设C1:$\frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1$,C2:$\frac{x^2}{{2{b^2}}}+\frac{y^2}{{4{b^2}}}=1$,由对称性,四个焦点构成的四边形为菱形,从而得到b2=1,由此能求出椭圆C1与C2的方程.
(Ⅱ)(1)设P(x0,y0),则$\frac{x_0^2}{2}+\frac{y_0^2}{4}=1$,$A(-\sqrt{2},0)$,$B(\sqrt{2},0)$,由此能证明直线PA,PB斜率之积为常数.
(2)设E(x1,y1),则$\frac{x_1^2}{2}+y_1^2=1$,${k_{EA}}=\frac{y_1}{{{x_1}+\sqrt{2}}}$,${k_{EB}}=\frac{y_1}{{{x_1}-\sqrt{2}}}$,由此能求出直线AF与直线BE的斜率之积为常数.
解答 (本小题满分12分)
解:(Ⅰ)∵椭圆C1与C2的中心在原点,焦点分别在x轴与y轴上,它们有相同的离心率$e=\frac{{\sqrt{2}}}{2}$,
并且C2的短轴为C1的长轴,C1与C2的四个焦点构成的四边形面积是$2\sqrt{2}$.
∴依题意$e=\frac{{\sqrt{2}}}{2}$,设C1:$\frac{x^2}{{2{b^2}}}+\frac{y^2}{b^2}=1$,C2:$\frac{x^2}{{2{b^2}}}+\frac{y^2}{{4{b^2}}}=1$,
由对称性,四个焦点构成的四边形为菱形,
且面积$S=\frac{1}{2}×2b×2\sqrt{2}b=2\sqrt{2}$,解得:b2=1,
所以椭圆C1:$\frac{x^2}{2}+{y^2}=1$,C2:$\frac{x^2}{2}+\frac{y^2}{4}=1$….(4分)
证明:(Ⅱ)(1)设P(x0,y0),
则$\frac{x_0^2}{2}+\frac{y_0^2}{4}=1$,$A(-\sqrt{2},0)$,$B(\sqrt{2},0)$,
${k_{PA}}=\frac{y_0}{{{x_0}+\sqrt{2}}}$,${k_{PB}}=\frac{y_0}{{{x_0}-\sqrt{2}}}$….(6分)
∴${k_{PA}}•{k_{PB}}=\frac{y_0^2}{x_0^2-2}=\frac{4-2x_0^2}{x_0^2-2}=-2$,
直线PA,PB斜率之积为常数-2….(8分)
解:(2)设E(x1,y1),则$\frac{x_1^2}{2}+y_1^2=1$,${k_{EA}}=\frac{y_1}{{{x_1}+\sqrt{2}}}$,${k_{EB}}=\frac{y_1}{{{x_1}-\sqrt{2}}}$,
∴${k_{EA}}•{k_{EB}}=\frac{y_1^2}{x_1^2-2}=\frac{{1-\frac{1}{2}x_1^2}}{x_0^2-2}=-\frac{1}{2}$,同理:${k_{FA}}•{k_{FB}}=-\frac{1}{2}$….(10分)
∴${k_{EA}}•{k_{EB}}.{k_{FA}}•{k_{FB}}=\frac{1}{4}$,
由kEA=kPA,kFB=kPB,结合(1)有${k_{EA}}•{k_{FB}}=-\frac{1}{8}$….(10分)
点评 本题考查椭圆方程的求法,考查两直线斜率之积为常数的证明,是中档题,解题时要认真审题,注意椭圆性质、直线方程、斜率公式等知识点的合理运用.

 阅读快车系列答案
阅读快车系列答案| A. | $(-\frac{1}{2},+∞)$ | B. | $(-\frac{1}{2},0)∪(0,+∞)$ | C. | $[-\frac{1}{2},+∞)$ | D. | [0,+∞) |
| A. | $\frac{2}{3}$ | B. | -1 | C. | 2 | D. | -1或2 |
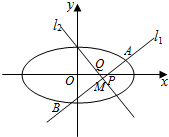 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(0,1),离心率为 $\frac{\sqrt{3}}{2}$,点O为坐标原点.