题目内容
4.过焦点在x轴上的椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{16}$=1的右焦点F2的直线交椭圆于A,B两点,F1是椭圆的左焦点,若△AF1B的周长为20,则实数m的值为( )| A. | 5 | B. | 25 | C. | 10 | D. | 100 |
分析 由题意可得椭圆的a=$\sqrt{m}$,由椭圆的定义可得AF1+AF2=BF1+BF2=2a,可得△AF1B的周长为4a,解方程可得m.
解答 解:由题意可得椭圆$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{16}$=1的a=$\sqrt{m}$,b=4,
由椭圆的定义可得AF1+AF2=BF1+BF2=2a,
即有△AF1B的周长为AB+AF1+AF2=AF1+AF2+BF1+BF2=4a,
由4$\sqrt{m}$=20,解得m=25.
故选:B.
点评 本题考查椭圆的定义、方程和性质,主要考查椭圆定义法的运用,考查运算能力,属于基础题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
15.已知椭圆C1,抛物线C2的焦点均在x轴上,从两条曲线上各取两个点,将其坐标混合记录于下表中:
(1)求椭圆C1和抛物线C2的标准方程;
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点.
①求证:直线PA,PF,PB的斜率成等差数列;
②若点P在x轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
| x | -$\sqrt{2}$ | 2 | $\sqrt{6}$ | 9 |
| y | $\sqrt{3}$ | -$\sqrt{2}$ | -1 | 3 |
(2)过椭圆C1右焦点F的直线l与此椭圆相交于A,B两点,若点P为直线x=4上任意一点.
①求证:直线PA,PF,PB的斜率成等差数列;
②若点P在x轴上,设$\overrightarrow{FA}$=λ$\overrightarrow{FB}$,λ∈[-2,-1],求|$\overrightarrow{PA}$+$\overrightarrow{PB}$|取最大值时的直线l的方程.
13.已知倾斜角为45°的直线l过抛物线y2=4x的焦点,且与抛物线交于A,B两点,则△OAB(其中O为坐标原点)的面积为( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 8 |
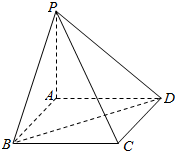 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{2}$.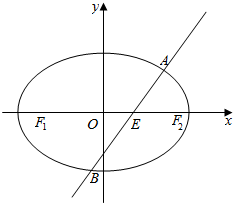 如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\sqrt{2}$.
如图,在平面直角坐标系xOy中,椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,直线l与x轴交于点E,与椭圆C交于A、B两点.当直线l垂直于x轴且点E为椭圆C的右焦点时,弦AB的长为$\sqrt{2}$.