题目内容
9．已知$cos（\frac{π}{4}+θ）=\frac{2}{3}\sqrt{2}$，则sin2θ=（ ）| A． | $-\frac{7}{9}$ | B． | $\frac{7}{9}$ | C． | $-\frac{8}{9}$ | D． | $\frac{8}{9}$ |
分析 由两角和的余弦展开已知式子，平方结合二倍角的正弦可得．
解答 解：∵$cos（\frac{π}{4}+θ）=\frac{2}{3}\sqrt{2}$，
∴$\frac{\sqrt{2}}{2}$cosθ-$\frac{\sqrt{2}}{2}$sinθ=$\frac{2}{3}$$\sqrt{2}$，
∴cosθ-sinθ=$\frac{4}{3}$，
平方可得1-2sinθcosθ=$\frac{16}{9}$，
∴sin2θ=2sinθcosθ=-$\frac{7}{9}$，
故选：A．
点评 本题考查三角函数化简求值，属基础题．
练习册系列答案
相关题目
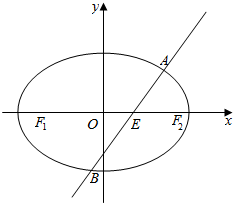如图，在平面直角坐标系xOy中，椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，直线l与x轴交于点E，与椭圆C交于A、B两点．当直线l垂直于x轴且点E为椭圆C的右焦点时，弦AB的长为$\sqrt{2}$．
（1）执行如图所示的程序框图，如果输入的t∈[-1，3]，若输出的s的取值范围记为集合A，求集合A；
4．函数$y=\frac{1}{lg（x-1）}$的定义域为（ ）
| A． | （-∞，1） | B． | （1，+∞） | C． | （1，2）∪（2，+∞） | D． | （1，3）∪（3，+∞） |
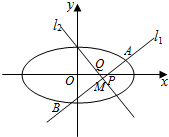已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（0，1），离心率为 $\frac{\sqrt{3}}{2}$，点O为坐标原点．
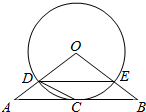如图，△ABO三边上的点C、D、E都在⊙O上，已知AB∥DE，AC=CB．