题目内容
16.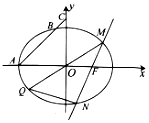 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F(1,0),过点A且斜率为1的直线交椭圆E于另一点B,交y轴于点C,$\overrightarrow{AB}=6\overrightarrow{BC}$.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,右焦点为F(1,0),过点A且斜率为1的直线交椭圆E于另一点B,交y轴于点C,$\overrightarrow{AB}=6\overrightarrow{BC}$.(1)求椭圆E的方程;
(2)过点F作直线l与椭圆E交于M,N两点,连接MO(O为坐标原点)并延长交椭圆E于点Q,求△MNQ面积的最大值及取最大值时直线l的方程.
分析 (1)求得B点坐标代入椭圆方程,即可求得a和b的值,求得椭圆方程;
(2)设直线方程,代入椭圆方程,由韦达定理,弦长公式及基本不等式的性质,即可求得△MNQ面积的最大值及直线l的方程.
解答 解:(Ⅰ)由题知A(-a,0),C(0,a),故$B(-\frac{a}{7},\frac{6a}{7})$,
代入椭圆E的方程得$\frac{1}{49}+\frac{{36{a^2}}}{{49{b^2}}}=1$,又a2-b2=1,
故a2=4,b2=3,
椭圆$E:\frac{x^2}{4}+\frac{y^2}{3}=1$;
(Ⅱ)由题知,直线l不与x轴重合,故可设l:x=my+1,
由$\left\{\begin{array}{l}x=my+1\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$得(3m2+4)y2+6my-9=0,
设M(x1,y1),N(x2,y2),则${y_1}+{y_2}=\frac{-6m}{{3{m^2}+4}},{y_1}{y_2}=\frac{-9}{{3{m^2}+4}}$,
由Q与M关于原点对称知,${S_{△MNQ}}=2{S_{△MON}}=|{y_1}-{y_2}|=\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}{y_2}}=\frac{{12\sqrt{{m^2}+1}}}{{3{m^2}+4}}$=$\frac{12}{{3\sqrt{{m^2}+1}+\frac{1}{{\sqrt{{m^2}+1}}}}}$,
∵$\sqrt{{m^2}+1}≥1$,
∴$3\sqrt{{m^2}+1}+\frac{1}{{\sqrt{{m^2}+1}}}≥4$,即S△MNQ≤3,当且仅当m=0时等号成立,
∴△MNQ面积的最大值为3,此时直线l的方程为x=1.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆方程位置关系,考查韦达定理,弦长公式,基本不等式的应用,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 可能有两支队伍得分都是18分 | B. | 各支队伍得分总和为180分 | ||
| C. | 各支队伍中最高得分不少于10分 | D. | 得偶数分的队伍必有偶数个 |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 4 |
| A. | (0,4) | B. | (-8,8) | C. | R | D. | (0,8) |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{50}$ |
| A. | $3\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{3}+1$ |
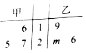 甲、乙两组数据的茎叶图如图所示,其中m为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为$\frac{3}{5}$.
甲、乙两组数据的茎叶图如图所示,其中m为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为$\frac{3}{5}$.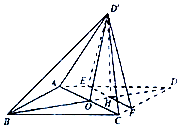 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.