题目内容
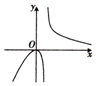
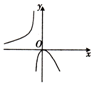
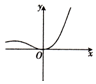
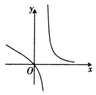
19.使函数f(x)=$\root{3}{{x}^{2}(1-{x}^{2})}$满足罗尔定理条件的区间是( )| A. | [0,1] | B. | [-1,1] | C. | [-2,2] | D. | [-$\frac{3}{5}$,$\frac{4}{5}$] |
分析 求导,由足罗尔定理条件,即可求得答案.
解答 解:对f(x)求导,得到f′(x)=$\frac{2x-4{x}^{3}}{3}$$\root{3}{{x}^{4}(1-{x}^{2})^{2}}$,
故点x=-1,0,1时,f‘(x)没意义.
罗尔定理条件:函数f(x)满足:(1)在闭区间[a,b]上连续(其中a不等于b);
(2)在开区间(a,b)内可导;
(3)在区间端点处的函数值相等,即f(a)=f(b),
上述选项都符合条件(1)和(3)满足,
但是要注意条件(2),是区间内每一个数都要可导(端点除外),
所以区间内不能有不可导的,即在闭区间对应的开区间中不含有这三个点中的任何一个.
故选A.
点评 本题考查足罗尔定理的应用,考查足罗尔定理条件,复合函数求导法则,考查转化思想,属于中档题.

练习册系列答案
相关题目
7.现有10支队伍参加篮球比赛,规定:比赛采取单循环比赛制,即每支队伍与其他9支队伍各比赛一场;每场比赛中,胜方得2分,负方得0分,平局双方各得1分.下面关于这10支队伍得分的叙述正确的是( )
| A. | 可能有两支队伍得分都是18分 | B. | 各支队伍得分总和为180分 | ||
| C. | 各支队伍中最高得分不少于10分 | D. | 得偶数分的队伍必有偶数个 |
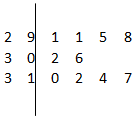 如图是根据我省的统计年鉴中的资料做成的2007年至2016年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到2007年至2016年我省城镇居民百户家庭人口数的平均数为303.6.
如图是根据我省的统计年鉴中的资料做成的2007年至2016年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到2007年至2016年我省城镇居民百户家庭人口数的平均数为303.6.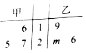 甲、乙两组数据的茎叶图如图所示,其中m为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为$\frac{3}{5}$.
甲、乙两组数据的茎叶图如图所示,其中m为小于10的自然数,已知甲组数据的中位数大于乙组数据的中位数,则甲组数据的平均数也大于乙组数据的平均数的概率为$\frac{3}{5}$.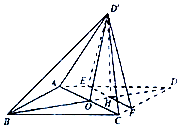 如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.
如图,菱形ABCD的对角线AC与BD交于点O,点E、F分别在AD,CD上,AE=EF,EF交BD于点H,将△DEF沿EF折到△D'EF的位置.