题目内容
16.已知正四面体ABCD的棱长为2,若动点P从底面△BCD的BC的中点出发,沿着正四面体的侧面运动到D点停止,则动点P经过的最短路径长为( )| A. | 3 | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{5}$ |
分析 由题意画出图形,剪展得到平面图形,利用余弦定理求得答案.
解答 解:如图,
由题意可知,动点P从底面△BCD的BC的中点出发,沿着正四面体的侧面运动到D点停止,
则动点P经过的最短路径为右图中的PD,
在△PBD中,∵BD=2,BP=1,∠PBD=120°,
∴$PD=\sqrt{{2}^{2}+{1}^{2}-2×1×2×cos120°}$=$\sqrt{5-4×(-\frac{1}{2})}=\sqrt{7}$.
故选:B.
点评 本题考查多面体表面上的最短距离问题,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
6.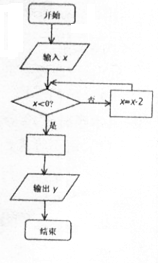 如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )
如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )
 如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )
如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )| A. | y=2-x | B. | y=2x | C. | y=x${\;}^{-\frac{1}{2}}$ | D. | y=x${\;}^{\frac{1}{2}}$ |
4.双曲线两焦点坐标分别为F1(0,-5),F2(0,5),2a=8,则双曲线的标准方程为( )
| A. | $\frac{x^2}{64}$-$\frac{y^2}{39}$=1 | B. | $\frac{y^2}{16}$-$\frac{x^2}{9}$=1 | C. | $\frac{x^2}{16}$-$\frac{y^2}{9}$=1 | D. | $\frac{y^2}{16}$-$\frac{x^2}{25}$=1 |
8.计算机是将信息转换成二进制进行处理的,二进制即“逢二进一”,如(1 101)2表示二进制数,将它转换成十进制数是1×23+1×22+0×21+1×20=13,那么将二进制数($\underset{\underbrace{11…1}}{14个}$01)2转换成十进制数是( )
| A. | 216-1 | B. | 216-2 | C. | 216-3 | D. | 216-4 |
9.已知函数f(x)=4x3-ax+1存在n(n∈N)个零点对应的实数a构成的集合记为A(n),则( )
| A. | A(0)=(-∞,3] | B. | A(1)={2} | C. | A(2)=(3,+∞) | D. | A(3)=(3,+∞) |