题目内容
1.已知圆x2+y2=4上有且只有四个点到直线12x-5y+m=0的距离为1,则实数m的取值范围是(-13,13).分析 求出圆心,求出半径,圆心到直线的距离小于半径和1的差即可.
解答 解:圆半径为2,
圆心(0,0)到直线12x-5y+c=0的距离小于1,即$\frac{|m|}{\sqrt{1{2}^{2}+{5}^{2}}}$=$\frac{|m|}{13}$<1,
则m的取值范围是(-13,13).
故答案为:(-13,13)
点评 此题考查了圆与直线的位置关系,圆心到直线的距离小于半径和1的差,此时4个,等于3个,大于这个差小于半径和1的和是2个.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.已知正四面体ABCD的棱长为2,若动点P从底面△BCD的BC的中点出发,沿着正四面体的侧面运动到D点停止,则动点P经过的最短路径长为( )
| A. | 3 | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{5}$ |
6.已知椭圆方程为$\frac{x^2}{16}$+$\frac{y^2}{9}$=1,椭圆上的点M到该椭圆的一个焦点F1的距离为2,N为MF1的中点,O是椭圆的中心,那么线段ON的长度为( )
| A. | 2 | B. | 3 | C. | 4 | D. | $\frac{3}{2}$ |
10.给出如图的程序框图,程序输出的结果是( )


| A. | 55 | B. | 56 | C. | 72 | D. | 46 |
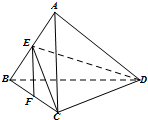 如图,已知空间四边形ABCD中,BC=AC,AD=BD,E,F分别是AB,BC的中点.
如图,已知空间四边形ABCD中,BC=AC,AD=BD,E,F分别是AB,BC的中点.