题目内容
11.由正数组成的集合A具有如下性质:若a∈A,b∈A且a<b,那么1+$\frac{a}{b}$∈A.(1)试问集合A能否恰有两个元素且$\frac{4}{3}$∈A?若能,求出所有满足条件的集合A;若不能,请说明理由.
(2)试问集合A能否恰有三个元素?若能,请写出一个这样的集合A;若不能,请说明理由.
分析 (1)先确定b=3a,再利用集合A恰有两个元素且$\frac{4}{3}$∈A,a=$\frac{4}{3}$或b=$\frac{4}{3}$,即可得出结论;
(2)利用反证法,即可得出结论.
解答 解:(1)由题意,1+$\frac{a}{b}$=$\frac{4}{3}$,∴$\frac{a}{b}$=$\frac{1}{3}$,∴b=3a,
∵集合A恰有两个元素且$\frac{4}{3}$∈A,
∴a=$\frac{4}{3}$或b=$\frac{4}{3}$,
∴b=4或a=$\frac{4}{9}$,
∴A={$\frac{4}{3}$,4}或B={$\frac{4}{3}$,$\frac{4}{9}$};
(2)由题意,3个元素为a,b,1+$\frac{a}{b}$,
若a<b<1+$\frac{a}{b}$,则1+$\frac{a}{1+\frac{a}{b}}$∈A,1+$\frac{b}{1+\frac{a}{b}}$∈A,
令1+$\frac{a}{1+\frac{a}{b}}$=a,可得a2-a-b=0,1+$\frac{b}{1+\frac{a}{b}}$=b,可得b2-b-a=0,
两方程相减可得a=b与已知矛盾,故集合A不能恰有三个元素.
点评 本题考查集合运算,考查新定义,考查学生的计算能力,比较基础.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
1.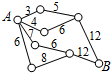 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 26 |
16.已知正四面体ABCD的棱长为2,若动点P从底面△BCD的BC的中点出发,沿着正四面体的侧面运动到D点停止,则动点P经过的最短路径长为( )
| A. | 3 | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{5}$ |
 已知函数f(x)=$\left\{{\begin{array}{l}{{x^2}-1,x<1}\\{-{{log}_2}x,x≥1}\end{array}}$.
已知函数f(x)=$\left\{{\begin{array}{l}{{x^2}-1,x<1}\\{-{{log}_2}x,x≥1}\end{array}}$.