题目内容
6.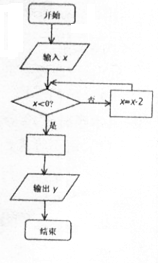 如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )
如图是一个算法程序框图,当输入的x的值为4时,输出的结果恰好是$\frac{1}{4}$,则空白处的关系式可以是( )| A. | y=2-x | B. | y=2x | C. | y=x${\;}^{-\frac{1}{2}}$ | D. | y=x${\;}^{\frac{1}{2}}$ |
分析 根据程序框图可知,程序运行时,列出数值x的变化情况,从而求出当x=-2时,输出$\frac{1}{4}$,从而得出答案.
解答 解:当x=4时,因为x>0,
所以x=x-2,即x=2≥0,
又x=x-2,即x=0≥0,
又x=x-2,即x=-2<0,
此时输出y=$\frac{1}{4}$;
所以方框内应填写y=2x.
故选:B.
点评 本题考查了当型循环结构,循环结构有两种形式:当型循环结构和直到型循环结构,当型循环是先判断后循环,直到型循环是先循环后判断,是基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
16.已知数列{an}是等差数列,若a1-a9+a17=7,则a3+a15=( )
| A. | 7 | B. | 14 | C. | 21 | D. | 7(n-1) |
1.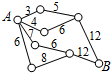 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
 如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
如图,小圆圈表示网络结点,结点之间的连线表示它们之间有网线连接,连线标注的数字表示该段网线单位时间内可以通过的最大信息量,现从结点A向结点B发送信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )| A. | 19 | B. | 20 | C. | 24 | D. | 26 |
16.已知正四面体ABCD的棱长为2,若动点P从底面△BCD的BC的中点出发,沿着正四面体的侧面运动到D点停止,则动点P经过的最短路径长为( )
| A. | 3 | B. | $\sqrt{7}$ | C. | 2$\sqrt{3}$ | D. | $\sqrt{5}$ |
