题目内容
已知x,y满足
,若使得z=ax+y取最大值的点有无数个,则a的值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出可行域,平移直线可知当直线与边界x-y+4=0重合时满足题意,由斜率相等可得.
解答:
 解:作出
解:作出
所对应的可行域(如图阴影),
变形目标函数可得y=-ax+z,
可知当直线y=-ax与直线x-y+4=0重合时,使得z=ax+y取最大值的点有无数个,
此时-a=1,解得a=-1
故答案为:-1
 解:作出
解:作出
|
变形目标函数可得y=-ax+z,
可知当直线y=-ax与直线x-y+4=0重合时,使得z=ax+y取最大值的点有无数个,
此时-a=1,解得a=-1
故答案为:-1
点评:本题考查简单线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
定义max{a,b}=
,设实数x,y满足约束条件
,且z=max{3x+y,2x-y},则z的取值范围为( )
|
|
A、[-
| ||
| B、[-4,6] | ||
| C、[-8,7] | ||
| D、[-4,7] |




 某学校招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高(单位:cm)编成如下茎叶图:若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“拿高个子”,如果用分层抽样的方法从“高小子”和“攀高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是
某学校招募了8名男志愿者和12名女志愿者,将这20名志愿者的身高(单位:cm)编成如下茎叶图:若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“拿高个子”,如果用分层抽样的方法从“高小子”和“攀高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是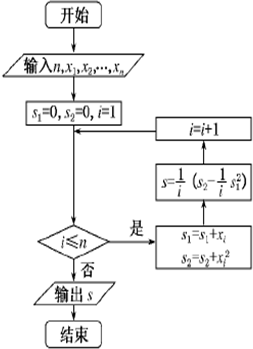 1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )
1,x2,…xn(单位:吨),根据如图所示的程序框图,若n=3,且x1,x2,x3,分别为1,2,3,则输出的结果S为( )