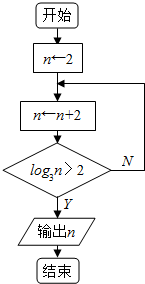
题目内容
1.若点 P(1,m)为抛物线y2=2px(p>0)上一点,F是抛物线的焦点,若|PF|=2,则m=±2.分析 根据抛物线上的点到焦点和准线的距离相等,可得p值,进而可得m值.
解答 解:∵点 P(1,m)为抛物线y2=2px(p>0)上一点,F是抛物线的焦点,
若|PF|=2,
则1+$\frac{p}{2}$=2,
解得:p=2,
故抛物线的方程为:y2=4x,将x=1代入可得:
m=±2,
故答案为:±2
点评 本题考查的知识点是抛物线的简单性质,难度不大,属于基础题.

练习册系列答案
相关题目
10.已知命题P的逆命题是“若a、b都不是偶数,则ab不是偶数”,则命题P的逆否命题是( )
| A. | 若a、b都是偶数,则ab是偶数 | |
| B. | 若ab是偶数,则a、b都是偶数 | |
| C. | 若a、b至少有一个是偶数,则ab是偶数 | |
| D. | 若ab是偶数,则a、b至少有一个是偶数 |
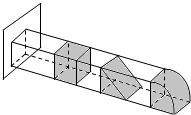 如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.
如图所示的三个几何体,一个是长方体,一个是直三棱柱,一个是过圆柱上、下底面圆心切下圆柱的四分之一部分,若这三个几何体的正视图和俯视图是相同的正方形,求他们的表面积之比.