题目内容
19.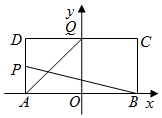 如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.
如图,在矩形ABCD中,|AB|=4,|AD|=2,O为AB中点,P,Q分别是AD和CD的中点,且直线AQ与BP的交点在椭圆E:$\frac{x^2}{a^2}$+y2=1(a>0)上.(Ⅰ)求椭圆E的方程;
(Ⅱ)设R为椭圆E的右顶点,T为椭圆E的上顶点,M为椭圆E第一象限部分上一点,求梯形ORMT面积的最大值.
分析 (Ⅰ)由题可知,$\frac{y_1}{2}=\frac{{{x_1}+2}}{4},\frac{y}{x+2}=\frac{2}{{{x_1}+2}},\frac{y}{x-2}=\frac{y_1}{-4}$,整理即可求得椭圆E的方程;
(Ⅱ)由${y_0}=\frac{1}{2}\sqrt{4-x_0^2}$,则四边形面积$S=\frac{1}{2}×2×{y_0}+\frac{1}{2}×1×{x_0}=\frac{{\sqrt{4-x_0^2}}}{2}+\frac{x_0}{2}≤\sqrt{\frac{4-x_0^2+x_0^2}{2}}=\sqrt{2}$,即可求得梯形ORMT面积的最大值.
解答 解:(Ⅰ)设AQ于BP交点C为(x,y),P(-2,y1),Q(x1,2),
由题可知,$\frac{y_1}{2}=\frac{{{x_1}+2}}{4},\frac{y}{x+2}=\frac{2}{{{x_1}+2}},\frac{y}{x-2}=\frac{y_1}{-4}$,(4分)
从而有$\frac{-4y}{x-2}=\frac{x+2}{y}$,整理得$\frac{x^2}{4}+{y^2}=1$,即为椭圆方程,
椭圆E的方程$\frac{x^2}{4}+{y^2}=1$;(6分)
(Ⅱ)R(2,0),设M(x0,y0),由${y_0}=\frac{1}{2}\sqrt{4-x_0^2}$,(8分)
从而所求四边形面积$S=\frac{1}{2}×2×{y_0}+\frac{1}{2}×1×{x_0}=\frac{{\sqrt{4-x_0^2}}}{2}+\frac{x_0}{2}≤\sqrt{\frac{4-x_0^2+x_0^2}{2}}=\sqrt{2}$,(10分)
当且仅当${x_0}=\sqrt{2},{y_0}=\frac{{\sqrt{2}}}{2}$取得最大值,
梯形ORMT面积的最大值$\sqrt{2}$.(12分)
点评 本小题考查椭圆的标准方程及面积最值问题,考查基本不等式的性质,考查学生的逻辑思维能力和运算求解能力,属于中档题.


| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
 秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 5 | B. | 12 | C. | 25 | D. | 50 |
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
| A. | 18 | B. | 24 | C. | 30 | D. | 60 |
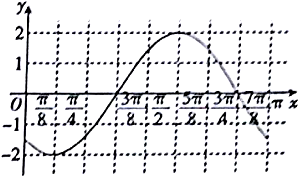 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.